Яков Перельман - Фокусы и игры

Из той же фигуры (рис. 2) так извлеките 8 спичек, не трогая других, чтобы оставшиеся спички составили 4 одинаковых квадрата.

В той же решетке (рис. 2) так уберите 6 спичек, не перекладывая остальных, чтобы осталось всего 3 квадрата.

И наконец, в той же фигуре (рис. 2) так уберите 8 спичек, не трогая остальных, чтобы осталось всего лишь 2 квадрата.

В фигуре, представленной на рис. 3, нужно так переложить 6 спичек с одного места на другое, чтобы образовалась фигура, составленная из 6 одинаковых четырехугольников.

Из 12 спичек нужно составить фигуру, в которой было бы три одинаковых четырехугольника и два одинаковых треугольника.

Как это сделать?

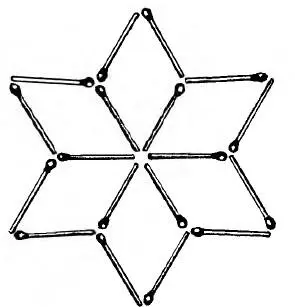
Рис. 3

Из 18 спичек нужно сложить два четырехугольника так, чтобы площадь одного была втрое больше площади другого. Спички, как и во всех предыдущих задачах, переламывать нельзя. Оба четырехугольника должны лежать обособленно, не примыкая друг к другу.

Если вам удалось решить предыдущую задачу, попытайтесь решить такую головоломку.

Из 18 спичек сложить два пятиугольника так, чтобы площадь одного была ровно втрое больше площади другого. Остальные условия те же, что и в предыдущей задаче.

На рис. 4 вы видите, как можно 19 целыми спичками ограничить шесть одинаковых участков.

А можно ли ограничить шесть одинаковых участков – хотя бы и иной формы -12 целыми спичками?

Рис. 4

1. Решение этой задачи на рис. 5.

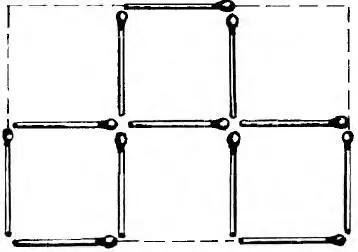
Рис. 5

2—5. Решение задачи 2 показано на рис. 6, задачи 3 на рис. 7 и 8, задачи 4 – на рис. 9, задачи 5 – на рис. 10.

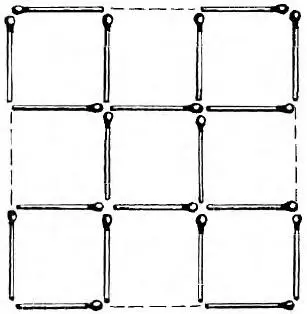
Рис. 6

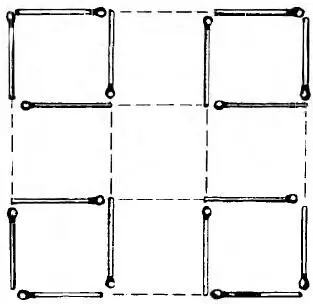
Рис. 7

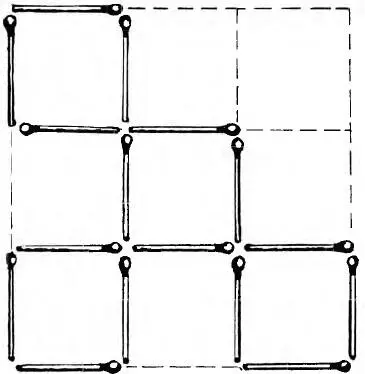
Рис. 8

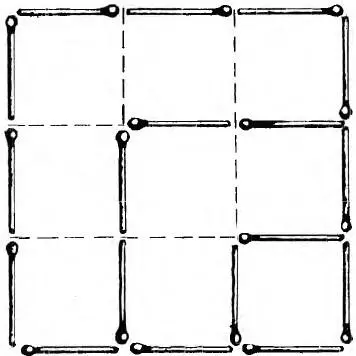
Рис. 9

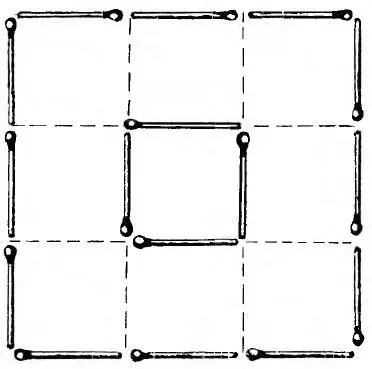
Рис. 10

6. Смотри на рис. 11.

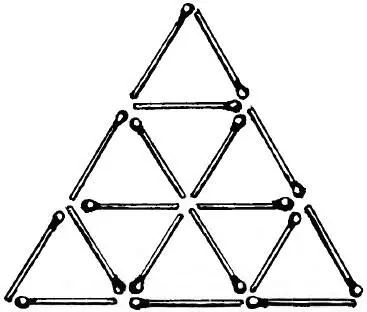
Рис. 11

7. Решение задачи 7 показано на рис. 12. Это равносторонний шестиугольник (но не правильный, поскольку его углы не равны).

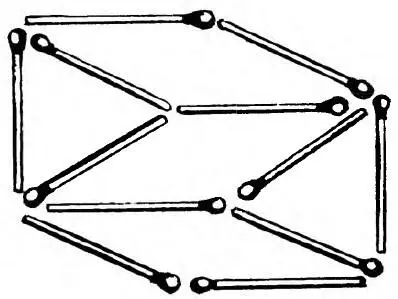
Рис. 12

8. Решение этой задачи показано на рис. 3. Площадь верхней фигуры образуют два квадрата, каждый со сторонами в одну спичку. Нижний четырехугольник представляет собой параллелограмм, высота которого AB = 1 1/ 2спички. Площадь параллелограмма по правилам геометрии равна его основанию, умноженному на высоту: 4 х 1^2 =6, т. е. втрое больше площади верхнего четырехугольника.

9—10. Решения задач 9 и 10 наглядно показаны на рис. 14 и 15.

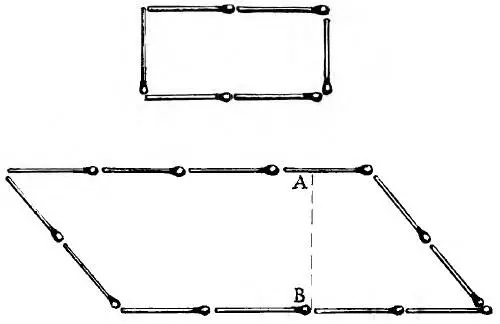
Рис. 13

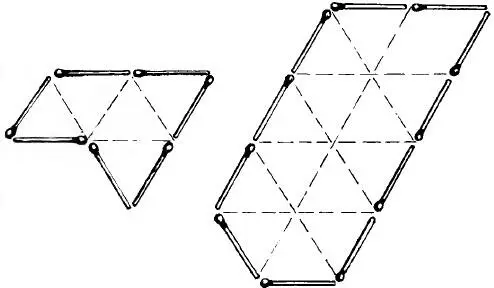
Рис. 14

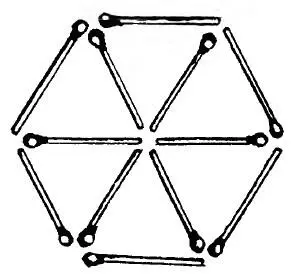
Рис. 15

– Чем вас так заинтересовала эта муха на кристалле?

– Своим странным поведением: она ходит по кристаллу, право, не без системы. Посмотрите, она путешествует только по ребрам и не ступает по граням. Что за охота ей ходить по острым ребрам, когда рядом сколько угодно плоских мест?

– Мне кажется, дело довольно просто. Чем склеены у вас грани кристалла?

Рис. 1. Муха на кристалле

– Вы подозреваете, что в клее есть что-то сладкое, привлекающее муху? Кажется, вы правы; она действительно вылизывает хоботком ребра кристалла. Так вот почему она медленно и систематически переходит с одного ребра на другое!

– И при этом на практике решает интересную задачу: обойти многогранник по его ребрам, не посещая дважды ни одного ребра.

– Разве это возможно?

– В данном случае вполне: ведь этот кристалл – восьмигранник.

– Да, октаэдр. И что же?

– У него на каждой вершине сходятся 4 ребра.

– Разумеется. Но какое отношение это имеет к нашей задаче?

– Самое непосредственное. Задача обойти все ребра многогранника, и притом не более чем по одному разу, разрешима только для тех многогранников, у которых в каждой вершине сходится четное число ребер.

– Вот как! Я об этом не знал. Почему же?

– Почему в каждой вершине должно сходиться именно четное число ребер? Очень просто. Ведь в каждую вершину надо попасть и надо из нее уйти, причем прийти по одной дороге, а уйти по другой, значит, нужно, чтобы в ней сходилась пара ребер. Если же, путешествуя по кристаллу, вы попадете на вершину вторично, если к ней ведет еще и третье ребро, то должно иметься непременно и четвертое, чтобы вы могли уйти с этой вершины, а не очутиться в тупике. Другими словами, число ребер, сходящихся в каждой вершине, должно быть парное, т. е. четное. Если хотя бы одна вершина многогранника имеет нечетное число сходящихся в ней ребер, то на такую вершину вы, конечно, можете, исчерпав все ведущие к ней парные ребра, попасть по последнему неиспользованному ребру, но покинуть эту вершину вам уже не удастся: путешествие здесь поневоле оборвется.

– Но ведь я могу просто не воспользоваться этим ребром, раз оно заведомо ведет в тупик!

– Тогда вы не выполните другого условия нашего путешествия: пройти по всем ребрам без исключения.

– Позвольте, но может же случиться, что это ребро как раз последнее и единственное, еще не пройденное. Тогда нет вовсе надобности покидать его: оно и будет конечной целью путешествия.