Яков Перельман - Математика в занимательных рассказах

Согласно новейшим исследованиям астронома Кертиса, самые далекие объекты Вселенной — спиральные туманности — расположены от нас на расстоянии 10 миллионов световых лет. Световой год, т. е. путь, проходимый светом в течение года, равен, круглым числом, 10 биллионам километров, т. е. 10 13км. Следовательно, радиус видимой Вселенной мы можем считать равным

10 13× 10 7= 10 20километрам,

или

10 20× 1000 = 10 23метрам.

Объем такого шара в куб. метрах равен

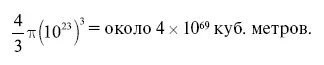
Считая по 1000 томов в куб. метре объема, узнаем, что Вселенная указанных размеров могла бы вместить только

4 = 10 69× 1000 = 4 × 10 72томов.

Следовательно, разделив все число томов «универсальной библиотеки» на это число, мы сократили бы ряд нулей на 73; разница между этим результатом и приведенным в рассказе, как видим, несущественна.

Примечание 3. Литературная машина

Поучительно рассмотреть придуманный Перельманом проект видоизменения идеи Лассвица, [31] Идея эта принадлежит, собственно, Лейбницу; Лассвиц лишь облек ее в форму рассказа. сущность которого ясна из следующего воображаемого разговора.

— В том виде, какой Лассвиц придал своей идее «универсальной библиотеки», она, конечно, неосуществима. Слишком уж велик размах: перебирать все комбинации из миллиона типографских знаков! Неудивительно, что получаются сверхастрономические числа. Другое дело — если ограничиться гораздо более скромными рамками.

— Например?

— Например, удовольствовавшись комбинациями всего лишь из 1000 литер, среди которых сто различных. Вообразим механизм, который систематически составляет все сочетания, возможные при наборе отрывка в 1000 литер. С каждого сочетания делаются оттиски. Что же мы получим?

— Ясно что: всевозможные образчики вздора и бессмыслицы.

— Да, но в этом море бессмыслицы неизбежно должны оказаться и все осмысленные сочетания литер. Это тоже ясно. Значит, у нас в руках очутятся все литературные отрывки, какие мыслимо написать тысячью литерами. А именно: по отдельным страницам, по полустраницам будем мы иметь все, что когда-либо было написано и когда-либо будет написано в прозе и стихах на русском языке и на всех существующих и будущих языках (потому что иностранные слова можно ведь передавать буквами русского алфавита). Все романы и рассказы, все научные сочинения и доклады, все журнальные и газетные статьи и известия, все стихотворения, все разговоры, когда-либо веденные всеми населяющими земной шар людьми и всеми прежде жившими (в том числе и наш нынешний разговор с вами), все интимные тайны, когда-либо кем-либо кому-либо доверенные, и все, что еще предстоит придумать, высказать и написать людям будущих поколений по-русски и в переводе на все языки, — все это без исключения будет в наших оттисках.

— Бесспорно так. Не забывайте, однако, что мы будем иметь разрозненные, беспорядочно перемешанные отрывки. Придется их еще подобрать и сопоставить.

— Конечно. Будет немало работы по отыскиванию разрозненных частей. Но эта работа сторицей окупится ценностью ее результата. Подумайте: без гениев искусства и науки, чисто механическим путем, мы получим величайшие произведения мировой литературы и науки, овладеем всеми будущими открытиями и изобретениями.

— Как же это осуществить? Как устроить вашу «литературную машину»?

— Тут-то и сказывается огромное преимущество моего проекта перед проектом Лассвица. Уменьшив число литер в 1000 раз, заменив толстый том одной страничкой малого формата, я достиг технической осуществимости этой замечательной идеи. То, что немыслимо сделать при миллионе литер, вполне возможно выполнить для тысячи.

— А именно?

— Довольно просто. Вообразите шестеренку, на ободе которой помещаются 100 необходимых нам литер. Высота и ширина литеры, скажем для простоты, 2 миллиметра. Окружность шестеренки в 2 × 100, т. е. в 200 миллиметров, имеет диаметр меньше 7 сантиметров. Толщина шестеренки может быть пошире литеры — ну, пусть в 4 мм. Вообразите 1000 таких шестеренок, насаженных рядом на одну общую ось. Получите вал длиною в 4 метра и толщиною в 7 см. Шестеренки соединены между собою так, как это делается в нумераторах и в счетных машинах, а именно: при полном повороте первой шестеренки — вторая повертывается на одну литеру, при полном повороте второй — третья повертывается на одну литеру, и так до последней, 1000-й шестеренки. Валик покрывается типографской краской и делает оттиски на длинной 4-метровой бумажной полосе. Вот и устройство «литературной» машины. Как видите, просто и не очень громоздко.

— Как же она работает?

— Шестеренки приводятся во вращение, как я уже сказал, последовательно. Сначала начинает вращаться первая и дает на бумаге оттиски своих литер — это первые 100 «литературных произведений» из категории бессмысленных. Когда она обернется один раз, она вовлекает во вращение вторую шестеренку: та повертывается на одну литеру и остается в этом положении, пока первая продолжает вращаться; получите еще 100 оттисков, теперь уже из двух букв. После 100 таких оборотов вторая шестеренка повертывается еще на одну литеру, опять обе дают 100 новых оттисков, и т. д. Когда же и вторая сделает полный оборот, присоединяется третья шестеренка, и получаются всевозможные оттиски из трех литер. И так далее, пока не дойдет очередь до последней, 1000-й шестеренки. Вы понимаете, что когда эта 1000-я шестеренка сделает полный оборот, все возможные комбинации в 1000 литер будут исчерпаны, и останется лишь работа по разборке оттисков.

— Много ли времени потребует вся работа вашей машины?

— Времени, конечно, порядочно. Но простота конструкции моей машины дает возможность значительно сократить необходимое время. Ведь работа машины сводится к вращению небольших шестерен, а скорость вращения можно технически довести до весьма высокой степени. Турбина Лаваля делает 30 000 оборотов в минуту. Почему бы и «литературную» машину не пустить таким темпом? Словом, как видите, у меня идея Лассвица получает конструктивное воплощение и притом в довольно простой форме — длинного ряда шестеренок, насаженных на одну ось и вращаемых с большою (но технически осуществимою) скоростью.

_____________________________________

Что мы должны думать об этом проекте «литературной» машины?

То, что он так же несбыточен, как и первоначальный проект Лассвица. Соорудить и пустить в ход эту «литературную» машину, пожалуй, вполне возможно, но дождаться конца ее работы человечество не сможет. Солнце погаснет, прежде чем последняя шестеренка закончит свое вращение. Действительно, при 30 000 оборотов в секунду

Надо ли продолжать? Если 12-я шестеренка начнет вращаться только через двести миллионов лет, то когда дойдет очередь до 1000-й? Нетрудно вычислить. Число минут выразится числом