Мартин Гарднер - Математические головоломки и развлечения

Игрок одерживает победу, когда его противник вынужден построить один из 105 возможных квадратов. В КВБ можно играть на доске фишками или на листе бумаги с карандашом в руках. В последнем случае нужно начертить доску и отмечать ходы крестиками и ноликами.

В течение нескольких месяцев после того, как я придумал эту игру, меня не покидала уверенность в том, что KBБ не может закончиться вничью. Позднее Г. М. Мак-Лури, студент-математик из Оклахомского университета, доказал, что ничья все-таки возможна.

Разделив 36 клеток на две группы по 18 клеток в каждой так, чтобы никакие четыре клетки, входящие в одну и ту же группу, не образовывали вершин квадрата, попробуйте показать, каким образом игра в КВБ может закончиться вничью.

2. Головоломка с маневровым тепловозом.Составление железнодорожных составов нередко приводит к трудным задачам из области исследования операций. Задача с маневровым тепловозом, изображенная на рис. 227, обладает тем достоинством, что сочетает в себе простоту формулировки с удивительной трудностью решения.

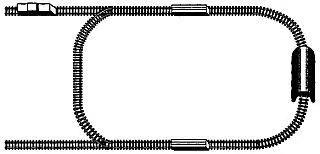
Рис. 227 Головоломка из области исследования операций.

Тоннель достаточно широк для того, чтобы через него свободно проходил тепловоз, но узок для вагонов. Задача состоит в том, чтобы, пользуясь тепловозом, поменять местами верхний и нижний вагоны и вернуть тепловоз в исходное положение. Тепловоз может тянуть и толкать вагоны спереди и сзади. Вагоны, если это необходимо, можно сцеплять друг с другом.

Лучшим считается решение, при котором требуемый результат достигается наименьшим числом операций. Под «операцией» здесь понимается любой пробег тепловоза между двумя остановками (останавливается тепловоз перед тем, как начать двигаться в обратном направлении, при подходе к вагону, который нужно толкнуть, или когда от него отцепляют вагон, который до того он тянул за собой). Перевод стрелок операцией не считается.

При решении задачи удобно пользоваться наглядной «моделью»: положив на рисунок три монеты различного достоинства, передвигать их по рельсам. Не нужно лишь забывать, что через тоннель может проходить только монетка, изображающая тепловоз. На рис. 227 вагон стоит слишком близко от стрелок. При решении задачи можно считать, что оба вагона расположены намного дальше «к востоку» и на отрезке пути, отделяющем их от стрелок, может разместиться тепловоз с другим вагоном.

Переводить стрелки «на ходу» не разрешается. Например, нельзя переводить стрелку в тот момент, когда тепловоз только протолкнул через нее не сцепленный с ним вагон, чтобы вагон покатился по одной ветке, а тепловоз, не останавливаясь, продолжал движение по другой.

3. Рекламные щиты на шоссе.Смит мчался на машине по шоссе с постоянной скоростью. Рядом с ним в кабине сидела его жена.

— Ты заметила, — обратился он к ней, — что эти надоедливые щиты с рекламой пива расставлены на одинаковом расстоянии друг от друга? Хотелось бы знать, на каком именно.

Миссис Смит посмотрела на часы и сосчитала, сколько рекламных щитов промелькнуло за окном в течение одной минуты.

— Какое странное совпадение! — воскликнул Смит. — Если это число умножить на 10, то получится в точности скорость нашей машины в милях в час.

Предположим, что скорость машины постоянна, щиты расставлены через правильные промежутки, а минута, отмеренная миссис Смит, начинается и кончается в моменты, когда машина находится как раз посреди расстояния, отделяющего один рекламный щит от другого. Спрашивается, чему равно это расстояние?

4. Как разрезать кубик и как разрезать бублик.Инженер, известный своей склонностью к геометрическим построениям, как-то раз пил кофе с бубликом. Прежде чем бросить в чашку кусочек сахара, имевший форму кубика, он положил его на стол и подумал: «Если я проведу горизонтальную плоскость через центр куба, то в сечении, разумеется, получится квадрат. Если я проведу плоскость через центр куба и четыре его вершины, то в сечении получится вытянутый прямоугольник. Если же я проведу плоскость вот так, то…».

К своему удивлению, инженер, мысленно представив себе форму сечения, ясно увидел, что оно имеет форму правильного шестиугольника.

Каким образом он провел секущую плоскость? Если длина ребра куба равна 0,5 дюйма, то чему равна сторона правильного шестиугольника?

Бросив кубик сахару в кофе, инженер обратил внимание на бублик, лежавший перед ним на тарелочке.

«Если я проведу через центр бублика горизонтальную плоскость, то в сечении получатся две концентрические окружности, — сказал он себе. — Если я проведу вертикальную плоскость, проходящую через центр бублика, то в сечении получатся две окружности, отстоящие друг от друга на расстояние, равное ширине дырки бублика. Если же я проведу плоскость вот так, то…». От удивления он даже присвистнул: сечение имело вид двух пересекающихся окружностей!

Как было проведено последнее сечение? Если бублик имеет форму идеального тора, наружный диаметр которого равен 3 дюймам, а дырка имеет поперечник в 1 дюйм, то чему равны диаметры пересекающихся окружностей?

5. Как разделить пополам инь и ян ?Два математика зашли пообедать в китайский ресторан «Инь и ян», расположенный на одной из улиц Манхэттена. Дожидаясь, когда их обслужат, они заговорили о символе, изображенном на карточке меню (рис. 228).

Рис. 228 Монада. Начало инь окрашено в черный цвет, а противоположное ему начало ян — в белый.

— Я думаю, это один из древнейших религиозных символов мира, — сказал один из них. — Вряд ли можно более наглядно и изящно изобразить противоположные начала, действующие в природе: добро и зло, мужчину и женщину, инфляцию и дефляцию, интегрирование и дифференцирование.

— Но этот же символ служит и фирменным знаком Северной Тихоокеанской железной дороги?

— Да. Я знаю, что один из главных инженеров компании видел эту эмблему на корейском флаге во время Чикагской всемирной выставки в 1893 году и уговорил правление сделать ее фирменным знаком. Он считал, что эта эмблема символизирует противоположность огня и воды, приводящих в движение паровоз.

— А как ты думаешь, не вдохновил ли этот древний китайский символ создателей современного бейсбольного мяча?

— Я бы не удивился, если бы узнал, что дело обстоит именно так. Кстати, ты знаешь, что существует изящный метод, позволяющий одной прямой разделить оба символа — инь и ян — на две равновеликие (по площади) части?