Мартин Гарднер - Математические головоломки и развлечения

Некоторые пытаются отделаться от парадокса Хемпеля смущенной улыбкой и недоуменным пожиманием плечами. Не следует забывать, однако, что многие логические парадоксы, которые долгое время считались пустыми забавами, безделушками, сыграли чрезвычайно важную роль в развитии современной логики. Точно так же анализ парадокса Хемпеля уже позволил глубоко проникнуть в существо некоторых сложных проблем индуктивной логики, основного средства получения всех научных результатов.

Вряд ли что-нибудь может произвести большее впечатление на математика, чем открытие связи между двумя на первый взгляд никак не связанными между собой математическими структурами.

Именно такое открытие сделал Д. У. Кроув. Он обнаружил связь между двумя популярными головоломками прошлого века — «Икосаэдрической игрой» и «Ханойской башней». Сначала мы расскажем о каждой головоломке в отдельности, а затем покажем ту неожиданную связь, которая существует между ними.

Игру с икосаэдром придумал в пятидесятых годах прошлого века знаменитый ирландский математик Уильям Р. Гамильтон. На примере этой игры он хотел продемонстрировать некоторые не совсем обычные свойства разработанного им исчисления, во многом схожего с принадлежащей тому же автору теорией кватернионов (предшественницей современного векторного анализа). Исчисление позволяло решать ряд сложных задач об обходе ребер пяти новых, тел, и в частности икосаэдра и додекаэдра. Гамильтон назвал свое исчисление икосаэдрическим, хотя в действительности в придуманной им игре приходится совершать обход ребер додекаэдра.

В 1859 году Гамильтон продал игру за 25 долларов одному лондонскому дельцу. Позднее она в различных видах появлялась в Англии и других европейских странах. Биограф Гамильтона сообщает, что эти 25 долларов были единственными деньгами, которые получил известный математик за свои открытия и научные труды.

Гамильтон придумал много игр и головоломок, связанных с додекаэдром, но самой интересной из них была следующая. Начав с любой вершины додекаэдра (каждой его вершине Гамильтон дал название какого-нибудь крупного города), нужно было совершить «кругосветное путешествие» — обойти ровно один раз все ребра правильного многогранника и вернуться в исходную вершину.

Иначе говоря, путь должен иметь вид замкнутой ломаной, составленной из всех ребер додекаэдра. Каждое ребро разрешается проходить только один раз. Начало и конец пути должны находиться в одной и той же вершине додекаэдра.

Представьте себе, что поверхность додекаэдра сделана из резины. Проткнув одну из его граней, растянем додекаэдр так, чтобы он целиком распластался на плоскости. Его ребра расположатся в виде сети, показанной на рис. 23.

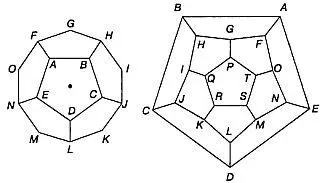
Рис. 23Додекаэдр (слева), проколотый (место прокола указано точкой) и растянутый на плоскости (справа). Размеры отдельных звеньев сети прямых на плоскости не совпадают с длиной ребер додекаэдра, но топологически сеть прямых на плоскости и сеть, образованная ребрами додекаэдра, эквивалентны.

Топологически эта сеть эквивалентна сети, образуемой ребрами «настоящего», несплющенного додекаэдра, но, разумеется, с плоской сетью обращаться намного удобнее, чем с объемной. Совершая «кругосветное путешествие» по этой сети («карте додекаэдра»), удобно отмечать каждую вершину, в которой вы побывали, фишкой.

Если все вершины додекаэдра эквивалентны, то существуют только два различных гамильтоновых пути, и любой из них является зеркальным отражением другого. Если же мы введем для каждой вершины особое обозначение и будем считать различными пути, проходящие через все 20 вершин в различном порядке, то таких путей окажется 30 (путь, проходимый в обратном направлении, мы не отличаем от пути, проходимого в прямом направлении). Гамильтоновы пути точно так же можно построить на четырех других Платоновых телах и на многих, хотя и не на всех, полуправильных многогранниках.

Известную игру «Ханойская башня» придумал французский математик Эдуард Люка. В 1883 году ее продавали как забавную игрушку. Первоначально она называлась «Профессор Клаус (Claus) из Коллеж Ли-Су-Стьян (Li-Sou-Stian)» но вскоре обнаружилось, что таинственный профессор из несуществующего коллежа — не более чем анаграмма фамилии изобретателя игры — профессора Люка (Lucas) из коллежа Сен-Луи (Saint Louis). Вид игрушки показан на рис. 24.

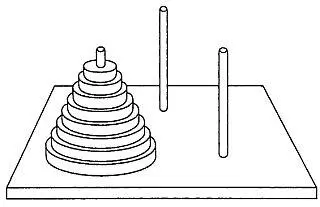
Рис. 24 «Ханойская башня»

Задача состоит в том, чтобы перенести пирамиду из восьми колец за наименьшее число ходов. За один раз разрешается переносить только одно кольцо, причем нельзя класть большее кольцо на меньшее.

Нетрудно доказать, что решение существует независимо от того, сколько колец в пирамиде, и что минимальное число необходимых перекладываний выражается формулой 2 n—1 (где n — число колец).

Таким образом, три диска можно перенести с помощью семи перекладываний; для четырех дисков понадобится пятнадцать перекладываний, для пяти — 31 и т. д. Для восьми колец, изображенных на рис. 24, потребуется 255 перекладываний. В первоначальном описании игрушка называется упрощенным вариантом мифической «Пирамиды браминов» в храме индийского города Бенареса. Как гласит предание, эта пирамида состоит из 64 золотых колец, которые и по сей день перекладывают жрецы храма. Как только им удастся справиться со своей задачей, храм рассыплется в пыль, грянет гром и мир исчезнет. О конце мира еще, пожалуй, можно спорить, но то, что храм за это время обратится в пыль, несомненно. Формула 2 64— 1 дает двадцатизначное число 18446744073 703551615.

Даже если бы жрецы работали не покладая рук, днем и ночью, перенося каждую секунду по одному кольцу, чтобы закончить работу, им понадобились бы многие миллионы тысячелетий.

(Получившееся число не является простым, но если число колец увеличить до 89, 107 или 127, то в каждом случае нужное число перемещений будет простым. Эти числа называются числами Мерсенна: простые числа, которые можно представить в виде 2 n— 1.

Сам Люка был первым, кто установил, что число 2 127— 1 простое.

Это огромное 39-значное число было самым большим из всех известных вплоть до 1952 года простых чисел. В 1952 году с помощью большой электронно-вычислительной машины было найдено пять новых чисел Мерсенна. Самое большое из них имеет вид 2 2281— 1.

Существует много аргументов в пользу того, что число 2 8191— 1 также простое, но пока это не доказано.)