Георгий Гамов - Занимательная математика

Сэм-младший попытался было объяснить отцу, что теория вероятностей далеко не исчерпывается вычислением вероятностей и что в ней разработаны весьма тонкие математические методы.

Сэм-младший усомнился даже в том, понимает ли Сэм-старший по-настоящему глубоко фундаментальные принципы теории вероятностей даже в простейших случаях вычисления благоприятных и неблагоприятных шансов, в чем Сэм-старший мнил себя непревзойденным знатоком.

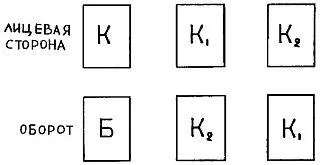
— Рассмотрим в качестве примера, — предложил Сэм-младший, — хотя бы следующую игру. Я кладу в шляпу три карточки: одну красную с обеих сторон, одну белую с обеих сторон и одну красную с одной стороны и белую с другой.

Предположим, что я извлекаю из шляпы одну карточку. Вынутая мной карточка обращена к нам красной стороной, какого цвета у нее другая сторона, мы не знаем.

— Ты хочешь, чтобы я догадался, какого цвета другая сторона? — спросил Сэм-Игрок.

— Совершенно верно, — согласился Сэм-младший. — Точнее говоря, ты должен сообщить мне, какова вероятность того, что у вынутой мною карточки другая сторона красная. Раз у вынутой мной карточки одна сторона красная, то она может быть только одной из двух карточек: либо красно-красной, либо красно-белой. Ты согласен?

— Согласен.

— Вот я и спрашиваю, какова вероятность того, что извлеченная мной карточка оказалась красно-красной? — заявил Сэм-младший.

Мог бы придумать задачу и посложнее, проворчал Сэм-старший. Простота предложенной сыном задачи вызывала у него отвращение. Ты мог извлечь из шляпы только две карточки, поэтому вероятность того, что у тебя в руке красно-красная карточка, равна одной второй.

— Я знал, что ты так и скажешь, — кивнул Сэм-младший, — но твой ответ неверен!

— Подумать только! И для этого твоя мать хотела, чтобы я послал тебя учиться в колледж! воскликнул Сэм-старший. — Уж не думаешь ли ты, что разбираешься в вероятностях лучше моего? Чтобы оценивать шансы «за» и «против», никакой математики не требуется.

Необходим лишь здравый смысл.

— Не сердись, — терпеливо увещевал разбушевавшегося родителя Сэм-младший. — Все дело в правильном определении вероятности.

Твой ответ подразумевает, что извлечена одна из двух возможных карточек, и что поэтому вероятность равна одной второй, но ты совсем не учитываешь условия задачи. Я сказал, что извлек из шляпы карточку с красной «лицевой» стороной. Чтобы вычислить вероятность того, что извлечена красно-красная карточка, я должен сначала спросить себя, сколькими способами я могу извлечь из шляпы карточку с красной стороной.

— Все это так, — согласился Сэм-старший, — но почему это меняет ответ?

— А вот почему, — терпеливо продолжал Сэм-младший. — У карточек в шляпе всего три красные стороны, а именно: две красные стороны у красно-красной карты и одна красная сторона у красно-белой карточки.

— А кто спорит? — возразил Сэм-старший.

— Но тогда ты должен признать, что существует три способа вытянуть карточку с красной лицевой стороной.

— Согласен.

— Прекрасно! А теперь рассмотрим подробнее те три способа, которыми я могу извлечь карточку с лицевой красной стороной. При одном способе оборотная сторона карточки белая, т. е. я извлек красно-белую карточку, в двух других случаях оборотная сторона карточки красная, т. е. в каждом случае я извлекаю красно-красную карточку. Таким образом, из трех возможных способов извлечь карточку с красной лицевой стороной в двух случаях оборотная сторона карточки оказывается красной и только в одном случае белой. Следовательно, вероятность того, что у извлеченной карточки оборотная сторона красная, равна двум третьим.

— Постой, постой! — усомнился Сэм-старший. Говоришь ты складно, но слишком быстро, и я не успеваю следить за твоими рассуждениями.

— Попробую доказать свое рассуждение иначе, — невозмутимо продолжал Сэм-младший. Ты согласился сыграть со мной в эту игру в предположении, что я извлек из шляпы карточку с красной лицевой стороной, но с тем же успехом мы могли бы сыграть в эту игру в предположении, что я извлек карточку с белой лицевой стороной.

— Разумеется, — кивнул Сэм-старший, — разницы никакой.

— Условимся теперь сыграть в новую игру, продолжал Сэм-младший. Если я извлеку карточку с красной лицевой стороной, то ты должен будешь определить вероятность того, что извлечена красно-красная карточка, а если я извлеку карточку с белой лицевой стороной, то ты должен будешь определить вероятность того, что извлечена бело-белая карточка. Суть проблемы на этом примере особенно ясна. Игра остается одной и той же, играем ли мы «на красное» или «на белое». Поэтому, играя на красное или на белое, мы получаем ту же самую вероятность, которую получили бы, играя только на красное или только на белое. А вот если бы мы вздумали играть на красное и на белое, то ответ был бы иным. Вопрос, который я задаю в действительности, звучит так: какова вероятность извлечь из трех карточек в шляпе карточку, обе стороны которой одного цвета, по сравнению с вероятностью извлечь карточку, стороны которой различного цвета? Ответ задачи в этом случае гласит, что вероятности относятся как 2:1, поскольку две карточки из трех имеют обе стороны одного цвета.

— Подумаешь! — произнес Сэм-старший, явно желая оправдать свою неудачу. — Ты просто придумал задачу-уродца. Такой место в кунсткамере. Я уверен, что на практике необходимость использовать строгое определение вероятности при решении настоящих задач никогда не возникает. К тому же никто не играет в игры с какими-то дурацкими карточками!

— В этом я как раз не уверен, — возразил Сэм-младший. — Я могу привести аналогичный пример с настоящими игральными картами.

— Великолепно! Действительно, почему бы нам не попробовать сыграть настоящими картами?

— Договорились. Предположим, что у тебя на руках обычная взятка из карт для игры в бридж. Одна карта во взятке — туз пик, остальные двенадцать карт совершенно случайны.

— Ты хочешь сказать, — уточнил Сэм-старший, что мы рассматриваем взятку только в том случае, если в ней есть туз пик?

— Совершенно верно, — подтвердил Сэм-младший. — Если взятка не содержит туза пик, мы ее просто не рассматриваем, а перетасовывеем колоду и сдаем другую взятку. Мы играем в нашу игру только в том случае если во взятке есть туз пик.

— Понял. Продолжай.

— Среди двенадцати остальных карт во взятке могут быть тузы других мастей, присутствие туза пик гарантировано, но существует ненулевая вероятность того, что в колоде в действительности два или больше тузов.