Дмитрий Лесной - Русский преферанс

а) у любого из игроков синглетная бубновая фигура и нет ни одного проноса;

б) две обрезные фигуры в бубне и нет двух проносов;

в) AKQв обрез и нет трёх проносов;

г) у Востока в бубне только одна фоска и фигура (или несколько фигур), ни одну из которых нельзя снести.

Проносы возможны при распределении пик 2:0 (два проноса) и/или треф 3:1 (один пронос) или 4:0 (два проноса). Соответственно две пики и три трефы на одной руке дают возможность пронести три бубны с другой руки.

Построим таблицу раскладов, при которых бубновый ВАЛЕТ НЕ ЛОВИТСЯ. [161]

Таблица вероятностей распределения всех мастей, существенного для поимки бубнового валета на мизере ( QJ10987 87(AК) J7 —)

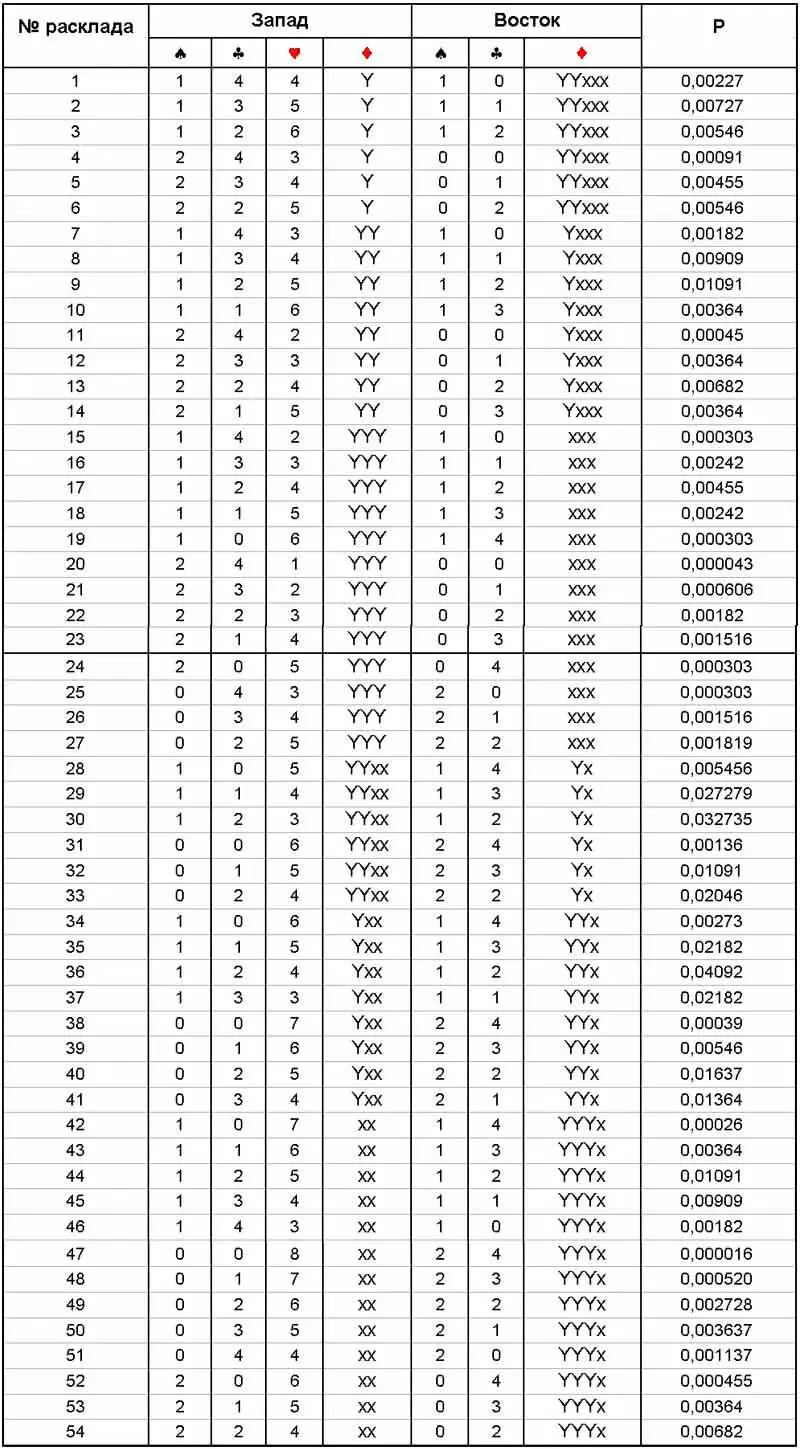
В раскладах № 1–27 не имеет значения, кто из вистующих имеет комбинацию обрезных фигур в бубне. Поэтому мы не стали воспроизводить в таблице ещё и 27 зеркальных вариантов с обрезными бубновыми фигурами у Востока, имея в виду, что при подсчёте нам будет достаточно умножить на два сумму вероятностей вариантов № 1–27.

Произведём эту часть расчёта. Суммируя все значения столбца P (вероятность расклада) для строк № 1–27, получаем 0,08385. Это число соответствует вероятности нахождения у Запада любой из перечисленных комбинаций обрезных бубновых фигур (т. е. без фосок). Поскольку наш валет не ловится также и при зеркальном расположении бубновых карт (обрезные фигуры у Востока), умножаем это число на два. Получаем 0,1677.

В нижней части таблицы (расклады № 28–54) перечислены варианты, в которых единственная фоска с фигурой или несколькими фигурами находится у Востока и нет возможности пронести все фигуры. Сумма вероятностей этих раскладов составляет 0,2660. Сложение с результатом первой половины расчёта даст число 0,4337. Это и будет вероятность того, что бубновый валет не ловится.

Следовательно, ловится он в 56,6 % случаев. Сравнивая с вероятностью поимки третьего трефового короля (58,2 %), приходим к выводу, что оставить валета немного лучше. Но обратите внимание, насколько возросла вероятность ловли валета за счёт побочных проносов (56,6 % вместо 43,8 %).

Мы не случайно потратили так много времени на составление таблицы вероятностей поимки именно этой комбинации — 7J. Она является пограничной. Все комбинации хуже 7J( 7Q, 7K, а также удлинённые «дырки» 7JQи т. д.) ловятся с ещё большей вероятностью. При этом (Внимание!) мы рассматривали боковые масти — пики и трефы — в не самом благоприятном для сносов распределении: пик — шесть, треф — две. При четырёхкарточной или пятикарточной боковой масти вероятность сноса по этой масти у противников выше. Таким образом, вывод следующий: любая «дырка» на мизере, начиная с комбинации 7J и хуже, делает назначение мизера неоправданным.

В главе «Оптимальные решения…»её автор, профессор Л. М. Литвин вводит понятие «граничной вероятности», т. е. такой вероятности, при которой математическое ожидание выигрыша при разных решениях проблемы одинаково. Например, при решении проблемы — сколько заказать на карте: AKQJ109 AKQx— нужно сравнить две вероятности: граничную, которая составляет 0,082 (для проблемы «десятерная или девятерная?»), и вероятность распределения треф 4:0, которое ведёт к подсаду на десятерной (вероятность выпадения четвёртого валета составляет 0,087). Если реальная вероятность подсада выше граничной, нужно заказать меньше (девятерную в последнем примере). Если ниже граничной — заказать по максимуму: возможные подсады на длинной дистанции окупятся.

Для мизера граничная вероятность составляет 0,5. Это означает, что любые мизера с вероятностью ловли (только на одну взятку!) выше 50 % — убыточны. Выбирая между третьим королём и вторым валетом, мы выбираем меньшее из двух зол. Если бы мы знали, что нам предстоит, лучше было от этого мизера отказаться.

Если интересно, давайте проверим, нужно ли было вообще идти на этот мизер. Если мы помним, Юг купил AK. Следовательно, до прикупа у него было: QJ10987 87 J7 —.

Сосчитаем вероятность удачной покупки. Для этого перечислим карты, покупка любой одной из которых делает мизер чистым: K, A, 9, 10, J, 8, 9, 7. При своём ходе мы добавили бы сюда 8, но ход Востока, поэтому будем считать только стопроцентные варианты. Итак, восемь карт из 22 для нас — «свои». Вероятность того, что одна из них будет первой картой из прикупа, составляет 8/22. Открыли первую карту прикупа — не наша! Теперь вероятность того, что вторая карта из прикупа «своя», составляет 8/21. Таким образом, вероятность того, что хотя бы одна будет «своей», составляет:

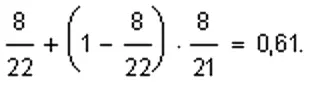
Так что идти на этот мизер, безусловно, стоило. Даже если бы вместо 7JЮг имел бы в бубне 7A.Не повезло, но — что делать?! — Юг играл правильно.

А если бы мы хотели посчитать математическое ожидание выигрыша этого мизера перед тем, как его заказать, мы должны были бы рассуждать следующим образом: в 61 случае из 100 мы купим свою и выиграем мизер наверняка; в 39 случаях мы не купим свою и будем иметь дырку не хуже 7J, которая ловится с вероятностью 0,57. То есть мы получим взятку (всегда не более одной) не в 39 случаях, а только в 22 случаях из 100 (39×0,57=22,23), а в 17 случаях выиграем мизер даже при плохой покупке (39×0,43=16,77). Таким образом, в 22 % случаев мы проиграем мизер с результатом одна взятка, а в 78 % случаев выиграем мизер. Если такая ситуация встретится нам 100 раз и мы всегда будем рассуждать таким образом, математически обоснованное решение принесёт нам на дистанции вистов выигрыша.