Сомерс Кларк - Строительство и архитектура в Древнем Египте

Таким образом, египетский метод умножения и деления представлял собой систему проб и ошибок, состоявших из удвоения, деления на две части и умножения на две трети. Сначала определяли две трети какого-то количества и уже на основе этого, в случае необходимости, вычисляли одну треть, одну шестую и т. д. Процесс определения двух третей от целого числа не представлял особых трудностей. Что касается дробей, то древний метод заключался в прибавлении половины к одной шестой части. Так, 2/ 3от 1/ 5равняется 1/ 10+ 1/ 30, аналогичным образом, 2/ 3от составляло 1/ 22+ 1/ 66. Почему египтяне в первую очередь не определяли одну треть нужного количества, мы не можем объяснить. Умножение на число, превышавшее 2 (за исключением 10), производилось, вероятно, очень редко. Папирус Ринд, представляющий собой более или менее продвинутую работу, почти не приводит примеров простого умножения или деления. Повсюду видно странное стремление все усложнять, и почти везде опущены этапы, очевидные для египтян, но часто непонятные для современного ума. Ниже приводятся примеры простого умножения и деления, выполненных древним способом, которые содержатся в папирусе Ринд и помогут читателям понять, в чем заключается проблема, поскольку ряд этапов в этих операциях опущен.

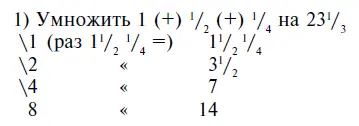
(Способ сложения дробей объясняется ниже.) [60]

2) Получить 49 из 11 (разделить 49 на 11) 1 (умноженное на 11 дает) 11

Два, полученное из 11, – это 1/ 6 1/ 66Найдено (см. таблицу дробей)

Сколько двоек укладывается в 5

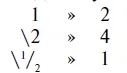
Ответ 2 1/ 2

Умножить 1/ 6 1/ 66на 2 1/ 2

Всего 2 1/ 2» Ответ: 1/ 3 1/ 11 1/ 33

Прибавить число 4 Конечный ответ 4 1/ 3 1/ 33.

Мы видим, что решение заключается в следующем: 1) сначала выясняют, сколько раз 11 содержится в 49 и каков остаток, 2) а затем, зная значение 2: 11, находят, умножая его на 2 1/ 2, значение остатка, или 5, разделенное на 11.

3) Задача № 30 из папируса Ринд

Если писец говорит тебе:

«10 стало 2/ 3 1/ 10от какого числа?

То пусть он услышит:

Ты используешь 2/ 3 1/ 10, чтобы определить 10 [61]

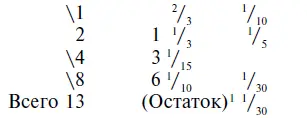
Всего, количество, которое называет это 13 1/ 23.

(Доказательство)

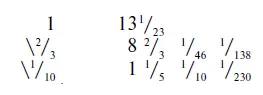
Всего 10

Следует отметить, что процесс сложения дробей и определения, каким образом дробь 2/ 3 1/ 10составляет 1/ 30, не приведены. Другие задачи, однако, приводят весь ход сложения дробей, который в принципе мало отличается от современного способа приведения их к общему знаменателю. В задаче № 32, приведенной в папирусе Ринд, необходимо сложить целый ряд дробей, чтобы доказать, что их сумма равна 1/ 4. Процесс решения заключается в следующем [62]:

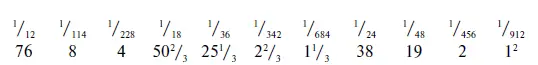
Всего: 228 (т. е.) 1/ 4

Профессор Пит объясняет ход решения тем, что «все дроби или делители, по-видимому, были приведены к самому большому делителю, а именно к 912: под каждой дробью красным написано число, показывающее, сколько раз число 912 входит в него. Как мы видим, это число не всегда является целым. Этот этап, должно быть, требовал подсчетов, которые в задачах на папирусе всегда опускаются. Красные числа суммируются и дают 228, которое представляет собой 1/ 4от 912. Таким образом, сумма всех дробей действительно составляет 1/ 4…».

В задаче № 30 папируса Ринд, которую мы привели выше, процесс сложения дробей гораздо более простой и, по-видимому, выглядел так:

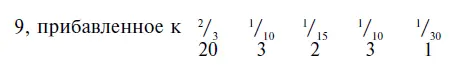
Сумма (для дробей) составляет 29, давая результат суммы дробей, равный единице без 1/ 30, а для всей задачи сумму, близкую к 10.

Второй этап решения задачи, который опускается при ее описании, заключается в определении, сколько раз 1/ 30входит в 2/ 3 1/ 10. Это выясняется путем обычного деления, и ход решения мог быть таким:

С другой стороны, вполне возможно, что египтянин мог сразу определить, что три раза по 1/ 30составляет 1/ 10, и его подсчеты могли быть такими:

Профессор Пит объясняет этот этап так: «Поскольку 2/ 3 1/ 10равно 23/ 30– а это действие полностью опущено, то ответ должен быть 1/ 23». Выполнение этого действия в ходе цепи рассуждений заставило, по-видимому, профессора решить, что египтянин понимал, что означает 23/ 30, или представлял себе эту дробь как 23 части из тридцати. Это является логическим выводом из его метода сложения дробей путем приведения их к общему знаменателю. Если бы это было так, он смог бы выразить эту дробь только в виде ряда множителей, который мог при необходимости восполнить дробью 2/ 3.

В папирусе Ринд приводится совершенно ненужное, с нашей точки зрения, число примеров умножения и деления, которое мы, с помощью алгебры, могли бы выразить несколькими пояснительными строчками или одной формулой. Причиной этого является тот факт, что задача, решаемая методом проб и ошибок, создает свои, только ей присущие трудности, причем некоторые из них требуют большой ловкости для разрешения.

Уравнения первой степени решались египтянами простым методом проб и ошибок. Знали они также и уравнения второй степени, в которых имелось одно неизвестное. В Берлинском папирусе приводится задача – разделить 100 квадратных локтей на два квадрата, стороны которых соотносились друг с другом как 1 к 3/ 4.

Знали египтяне и возведение во вторую степень, и извлечение квадратных корней. Первый процесс – это простое умножение, второй же заключался для самых простых чисел в длинной серии проб. В Берлинском папирусе приводятся квадратные корни для 6 1/ 4и 1 1/ 2 1/ 16.

Хотя древнее значение соотношения длины окружности к ее диаметру, или число п, и не встречается в математических папирусах, однако в папирусе Ринд дан пример (№ 50) определения площади круга. Способ заключался в вычислении 1/ 9диаметра и возведении полученного числа во вторую степень. Сейчас мы выразили бы это формулой A = ( 8/ 9D) 2. Эта формула дает значение, близкое к реальному. Египтяне получили площадь круга, равную 0,7902 D 2, тогда как в реальности она составляет 0,7854 D 2. Эта площадь, вероятно, была определена таким образом: на разделенной на квадраты поверхности был нарисован круг и подсчитано число квадратов, попавших в него.