Игорь Апокин - Чарльз Бэбидж 1791—1871

При сложении двух или более чисел на колонках может не остаться места для записи результатов суммы. Это происходит от недосмотра при подготовке или обработке карт, или когда расчет при решении математических проблем требует записи, превышающей возможности машины. В любом случае машина на это реагирует звуковым сигналом и останавливается.

Операция сложения в аналитической машине должна выполняться за один оборот главной оси, прерывистые периодические движения производятся эксцентриками на главной оси. Эксцентрики представляют из себя плоские диски с выступающими частями, действующими на рычаги с роликами на конце. Каждый эксцентрик должен быть двойным, т. е. иметь два ушка, причем выступ на одном соответствует впадине на другом. Такие эксцентрики довольно легко выполняются, устанавливаются и регулируются. Для выполнения операций сложения достаточно установить шесть-семь штук. На рис. 4 показан такой эксцентрик вместе с механизмом зацепления.

Рис. 4. Механизм зацепления аналитической машины

В центре внимания Бэбиджа при конструировании аналитической машины находились вопросы, связанные с выполнением операций в арифметическом устройстве.

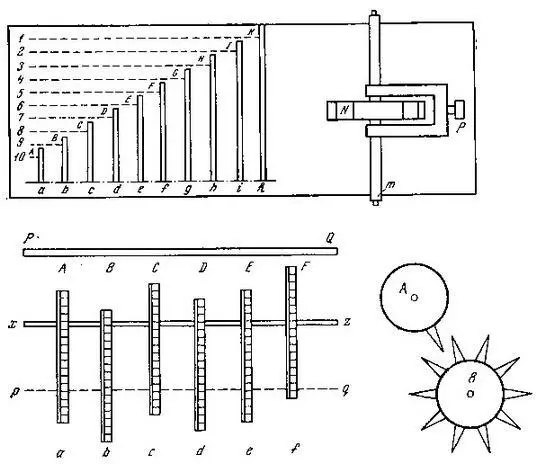
Рис. 5. Схема выполнения операции сложения в аналитической машине

Особенно много внимания, как отмечалось выше, было уделено ускорению операции сложения. В аналитической машине сложение является основной (базовой) операцией, поскольку механизм, сконструированный для ее эффективного выполнения позволял (при сравнительно простой модификации) осуществлять другие операции.

Конструктивно суммирование двух чисел выполняется в арифметическом устройстве следующим образом. Представим себе десять ребер переменной длины от А а до Кк, размещенных на пластине (рис. 5, верхний). Вилка Р входит в зацепление с колесом N по оси m квадратного сечения. Если вилка Р находится, например, напротив цифры 6, а колесо, вращаясь, свободно перемещается вдоль пластины, то оно повернется на расстояние, соответствующее шести зубцам, а его движение передается механизму счетного устройства.

Одно число может быть сложено с любой суммой, уже подсчитанной в машине, соответствующим расположением ребер Aa, Bb и т. д. (рис. 5, слева внизу). Когда пластина PQ передвигается вниз к закрепленной пластине xz с отверстиями для ребер, цилиндрические прямозубные колеса (на рисунке не показаны) на оси pq поворачиваются на число зубьев, зависящих от положения ребер. Если колеса на pq находятся в состоянии, соответствующем, например, числу 543243, а ребра расположены (как на рисунке) в положении суммирования числа 314236, то новая сумма будет 857479. Перенос при этом может осуществляться путем прерывистого движения шестерен (внизу справа на рисунке), среди которых шестерня В будет перемещаться на 1/10 оборота при каждом обороте однозубого колеса А.

Вычитание в машине обеспечивается введением дополнительной шестерни, которая осуществляет реверс (обратный поворот) цифровых дисков: при этом, проходя перед окошком, цифры последовательно уменьшаются, и всякий раз, когда 0 проходит и появляется 9, происходит перенос. При вычитании производятся те же самые операции и используется тот же самый принцип зацепления. Таким образом, один и тот же механизм служит для сложения и вычитания; смена операций производится перемещением одного рычага.

Следует отметить, что при вычитании большего числа из меньшего должно быть сделано указание о месте нахождения высшего разряда. Это необходимо для переноса к месту слева от высшего разряда числа и в тех случаях, когда нужно пройти через ноль; если такое указание не было сделано, раздается звонок и машина останавливается.

Для аналитической машины было разработано и нарисовано несколько вариантов выполнения операции умножения. Один из них относится к умножению многоразрядных чисел с помощью последовательных сложений. Для машины этот метод был подробно разработан, причем был подготовлен ряд чертежей, поясняющих действие механизмов.

При перемножении двух чисел, каждое из которых с любым числом знаков от одного до тридцати, необходимо для экономии времени установить, какой из сомножителей имеет меньшее число значащих цифр. Для этого были разработаны специальные механизмы, названные цифровыми счетными устройствами. Меньшее из двух чисел становится множителем. Оба числа вводятся в арифметическое устройство и размещаются на соответствующих колонках. При выполнении умножения способом последовательных сложений цифры множителя соответственно уменьшаются до нуля; во время проведения операции для любой одной цифры множителя эксцентрик на его колесе выталкивает рычаг, который разрывает связь и систему зацепления для сложения, происходит просто ход; при этом следующий оборот главной оси связан с ходом вместо сложения; затем связи восстанавливаются, и последовательные сложения продолжаются.

Умножение должно обычно производиться от высшего разряда к низшему. Произведение^ обычно содержит накопленную ошибку вследствие округления цифр в каждом числе, с которым продолжают работать. Если тем не менее при записи числа последовательных сложений, которые в конце умножения должны давать сумму всех цифр множителя, известна максимально возможная ошибка, то при необходимости иметь точный результат должна быть проведена коррекция. Например, машина может быть использована для деления пополам некоторого числа и сложения этой величины с последними цифрами результата, где бы он ни был округлен.

Бэбидж разработал несколько вариантов выполнения операций деления на машине, в том числе при помощи таблиц. Все разработки сопровождались теоретическими расчетами и рисунками. Наиболее эффективным оказался метод последовательного вычитания: делитель и делимое вводятся в счетное устройство, затем производится последовательное вычитание, число вычитаний записывается.

Бэбидж впервые предложил идею программного управления ходом вычислений. В связи с этим самой важной характеристикой аналитической машины, которую не оценил сам ученый, стала возможность выполнения команды, получившая в настоящее время название команды условного перехода.

[1 Математически условный переход представляет собой операцию вида:

A = A mпри ω =1

и A i+ 1 при ω = 0,

где A i— адрес команды с кодом условного перехода, хранящийся в счетчике команд (СК); А m— адресная часть команды, находящаяся в регистре команд (РК); ω — признак результата предыдущей операции. При ω = 0 происходит увеличение содержимого СК на единицу и переход к следующей команде, при ω = 1 — засылка в СК адреса команды, находящейся в РК, и переход к требуемой части программы.]