Владимир Арнольд - Истории давние и недавние

В этой истории, я думаю, виноват более всего снобизм Харди и его бурбакистская бесчеловечность, которые не позволили ему навестить своего больного ученика, жившего в одном с ним доме, и вовремя дать ему элементарные практические советы. Однако индийские коллеги, рассказавшие мне эту историю, и тактично избегая обсуждения английских нравов, связывали причину смерти Рамануджана с индийскими обычаями, по которым его жена осталась в Мадрасе, а не поехала с ним: ведь она должна была заботиться там о своей свекрови, матери Рамануджана — эта обязанность важнее, чем забота о муже!

С тех пор индусские студенты в Кембридже передают друг другу, как надо расстилать постель, и больше уже не замерзают. Странно, правда, что, несмотря на эти одеяла, вклад Рамануджана в математику остался непревзойдённым: его имя стоит рядом с именами Абеля и Галуа.

Один из самых знаменитых результатов Рамануджана связывает не вычислимые по отдельности (даже через числа π и е ) слагаемые

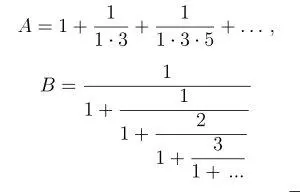
удивительной формулой для их суммы: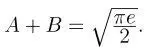

Вот пример удивительных открытий Рамануджана — его теоремы о делимости чисел разбиений.

Для любого натурального числа n обозначим через р(n) число различных разбиений числа и на натуральные слагаемые. Например, р (3) = = 3, как это показывают три разбиения (других нет):

3 = 3, 3 = 2 + 1, 3 = 1 + 1 +1.

Числа разбиений при n = 1, 2, 3…. образуют последовательность

р(n) = 1, 2,3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176….

которая много изучалась, начиная с Эйлера, связавшего её с теорией степенных рядов и градуированных колец в своём «Введении в анализ».

Рост этой последовательности при больших и описывается асимптотической формулой Харди-Рамануджана-Радемахера

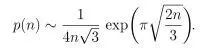
Согласно майору британской артиллерии МакМагону,

р (200) = 3 972 999 029 388.

(Это число можно вычислить по дающему большую точность приближению в правой части формулы.)

В этой формуле всё удивительно: в левой части стоит целое число чисто комбинаторного происхождения, задающее, сколькими способами можно разбить n на слагаемые.

В правой части стоит комбинация квадратного корня и экспоненциальной функции, в которой вдобавок участвуют иррациональные числа: π = 3,14… (задающее отношение длины окружности к её диаметру) и число Непера е = 2,718… (являющееся основой всего математического анализа).

То, что левая часть с большой точностью вычисляется по такой формуле, — совершенно удивительное открытие, где ярко проявляется фундаментальное единство всех частей математической науки: алгебры, геометрии, анализа, комбинаторики, теории вероятностей и техники приближенных вычислений.

Открытия Рамануджана делимости чисел разбиений состоят, например, в следующем:

числа р(5 n + 4) [это 5, 30, 135…] делятся на 5.

Математика — экспериментальная наука, и свои открытия Рамануджан сделал, экспериментируя с приведённой выше последовательностью.

Восхищаясь гением Рамануджана, я всё же больше люблю чем-то более близких мне Абеля и Литлвуда. Доказательство Абеля неразрешимости в радикалах алгебраических уравнений степени 5 и выше я в 1963 году перевёл на топологический язык теории римановых поверхностей и групп монодромий накрытий — это доказательство я рассказал тогда московским школьникам, и один из них впоследствии издал это доказательство в виде книжки (В.Б. Алексеев. «Теорема Абеля в задачах и решениях» — М.: Наука, 1976). Поэтому в 2001 году один талантливый польский математик (долго обучавшийся в Москве) опубликовал по-английски своё «новое топологическое доказательство теоремы Абеля» в журнале «Топологические методы в нелинейном анализе».

Экологи и этологи давно уже начали исследование того, как решают мальтузианскую проблему животные различных видов. Было обнаружено, что ещё до того, как положение с пищей становится катастрофическим, наблюдается на первый взгляд странное поведение (вроде похода грызунов к морю, где они и утопают), целесообразное не для отдельной особи, но лишь для сохранения вида.

К сожалению, я забыл имена авторов открытий, о которых прочитал в одном из московских научно-популярных журналов (не помню даже, была ли это «Наука и жизнь», «Знание — сила», «Техника — молодежи», «Природа» или «Химия и жизнь»).

Первый случай — отлёт саранчи, порой за тысячи километров. Поразительно здесь то, что улетают не те особи, которые увидели, что их стало слишком много на ближнем поле, а лишь их дети. При этом даже и не обязательно, чтобы их действительно стало много. Можно просто расставить по полю уголковые отражатели, как на аэродроме, отражающие зеркальный образ зрителя, с какой бы стороны он ни подошёл. Тогда саранча примет свои собственные многочисленные отражения за соседних родственников. И в результате следующее поколение — дети — улетят.

Как именно родители передают детям знание о том, что надо улетать, неясно, но во всяком случае не речью и не показом. По-видимому, передача происходит химическим путем. Возможно даже, что достаточно накормить молодёжь особями, видевшими многочисленных «соседей», — тогда молодёжь захочет улететь, соберется в стаю и улетит.

Второй пример — олени. Когда в лесу их становится слишком много, они делятся на две группы. Первая группа — более настырные особи — захватывают лучшие угодья, где хватит пищи и им, и их потомкам.

Вторая группа — менее настырные — уходят на неудобные пастбища и там ведут тихую и мирную жизнь. По-видимому, они играют в весёлые игры, перепрыгивают друг через друга, занимаются наукой и философией, поют и сочиняют стихи — на вид они совершенно счастливы, и самое главное отличие от настырных их родственников состоит в том, что они вовсе не размножаются и не приносят потомства. В результате еды для всех хватает и олений род в лесу сохраняется.

Мало кто знает подмосковные клюквенные болота, но я давно отыскал их и практически каждую осень набираю ведро-другое клюквы километрах в десяти от дома, среди сосновых лесов междуречья Истры и Москвы-реки.

Последнее время поблизости появились дачные поселки, да и поляны внутри леса начали застраиваться; думаю, что это — преступление против лесоохранных законов, но члена соседнего сельсовета, пытавшегося протестовать, недавно застрелили подъехавшие на машине заинтересованные граждане. Новые жители, кажется, не разбираются в дарах леса, так что мои соперники на грибных и ягодных местах — давно уже знакомые мне крестьяне соседних деревень.