Жозе Фаус - Наука. Величайшие теории: выпуск 3: Гейзенберг. Принцип неопределенности. Существует ли мир, если на него никто не смотрит?

«В этой статье мне прежде всего хотелось бы показать на простейшем примере нерелятивистского свободного атома водорода, что обычные правила квантования могут быть заменены другими положениями, в которых уже не вводится каких-либо «целых чисел». Эти целые числа выводятся естественным образом, подобно целому числу узлов при колебаниях струны. Это новое представление может быть обобщено, и я верю, что оно тесно связано с истинной природой квантования».

В формулировке, которая была предложена Эрвином Шрёдингером в 1925 году, состояние системы взаимодействующих частиц полностью описывается ее волновой функцией (ψ), которая зависит от времени и координат частиц. Если опустить релятивистские эффекты, то волновая функция будет решением уравнения

ihψ=Hψ

Рассмотрим использованные символы. Буква i обозначает мнимую единицу, то есть sqrt(-1). Буква h – редуцированную постоянную Планка h/2π. Точка над буквой, обозначающей функцию, – сокращенный способ обозначения производной по времени. В правой части уравнения записана функция Гамильтона H = T+V, равная сумме кинетической и потенциальной энергии системы. При рассмотрении электрона в атоме водорода кинетическая энергия, которая в классической физике определяется как Т = р²/(2m), задается оператором

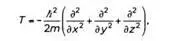
в котором содержатся вторые дифференциалы волновой функции относительно пространственных координат (х, у, z). Потенциальная энергия рассчитывается по закону Кулона: V= -е² /r. Шрёдингер был весьма удивлен появлению числа i, так как был убежден в «вещественности» волновой функции. К одной из своих статей он добавил комментарий, в котором упомянул Паули и его особое чувство юмора:

«Откуда мог взяться sqrt(-1) в этом уравнении? Возможный ответ, который я не осмелюсь привести здесь в общем виде, дал физик, который некоторое время назад покинул Австрию, но […] не оставил свой утонченный венский юмор и всегда умеет найти подходящее слово. Его ответ был таков: sqrt(-1) «проскользнул» в уравнение (4"), словно бы мы дали ему проскочить туда случайно. Тем не менее эта случайность заставила нас почувствовать огромное облегчение».

На языке математики электрон в атоме описывается волновой функцией, обозначаемой греческой буквой (пси). Эта функция является решением дифференциального уравнения в частных производных, которое называется уравнением Шрёдингера.

Возможно ли, что природа столь абсурдна, как нам кажется во время экспериментов по атомной физике?

Этим вопросом часто задавался Гейзенберг после обсуждения квантовой механики с Бором.

Эйнштейн написал Шрёдингеру такие строки: «Я убежден, что вы, предложив свою формулировку квантового состояния, совершили решающий прорыв, равно как я убежден в том, что метод Гейзенберга – Борна ошибочен». Однако Эйнштейн оказался неправ: сам Шрёдингер отмечал, что матричная и волновая механика с математической точки зрения абсолютно эквивалентны, несмотря на различия в предпосылках, идеях и методах. В матричной механике электрон считается частицей. Классические непрерывные переменные в ней заменялись матрицами, зависящими от двух целочисленных индексов, а классические уравнения замещались алгебраическими. Волновая механика – это, напротив, теория непрерывного, в которой электрон рассматривается как волна. Динамическое уравнение – это уравнение в частных производных, содержащее загадочные квантовые условия старой классической квантовой теории. Однако и матричная, и волновая механика приводили к одинаковым результатам. Как подчеркнул Шрёдингер, превосходство одной теории над другой было «по сути, второстепенным вопросом, связанным с удобством вычислений».

Эквивалентность матричной и волновой механики независимо друг от друга доказали два физика: Паули ограничился тем, что сообщил об этом Йордану в письме, а американский физик Карл Эккарт опубликовал свое доказательство в научном журнале. Подобное часто происходило в науке: когда несколько ученых одновременно работают над одной задачей, они могут найти решение независимо друг от друга и даже предложить совершенно разные формулировки основной идеи новой теории. И действительно, за короткий период было создано несколько различных формулировок квантовой механики. К примеру, необычные правила умножения, описанные Гейзенбергом, в которых результат зависит от порядка множителей, привлекли внимание английского физика Поля Дирака, который сразу же увидел в них аналогию со скобками Пуассона – одним из способов записи классических уравнений движения. На основе этой аналогии Дирак разработал собственную квантовую механику. Борн получил копию рукописи Дирака вскоре после того, как Гейзенберг и Йордан завершили строгое описание матричной квантовой механики. «Я прекрасно помню, что это стало одним из величайших сюрпризов во всей моей научной работе». И действительно, многие результаты, полученные в Гёттингене, Дирак вывел совершенно иначе. Спустя некоторое время, в 1926 году, Дирак и Йордан, вновь независимо друг от друга, разработали более общую формулировку, в которой состояния и наблюдаемые величины описывались соответственно с помощью векторов и операторов в рамках гильбертового пространства. Матричная и волновая формулировки представляли собой частные случаи этой абстрактной концептуальной схемы. Позднее, в 1942 году, Ричард Фейнман в своей докторской диссертации представил еще одну формулировку квантовой механики, в которой одновременно рассмотрел все возможные траектории, вдоль которых следует частица при перемещении из одной точки в другую. Как видите, фундаментальные физические законы могут быть сформулированы разными, но полностью эквивалентными способами.

Шрёдингер считал, что его волновая механика поможет разрешить проблему квантовых скачков. Для него волновая функция электрона в атоме водорода должна была включать суперпозицию волн с очень близкими частотами, которые на техническом языке называются волновым пакетом. Объем, связанный с этим пакетом, должен был в некотором роде соответствовать размеру электрона. Шрёдингер был убежден, что квантовый переход – это простой обмен энергией между двумя различными видами колебаний. Для него эта модель больше соответствовала интуитивным представлениям, чем электрон, «перепрыгивающий» с одного уровня на другой. Однако эта интерпретация была несогласованной, так как волновой пакет со временем расширяется и в конечном итоге электрон должен будет занять все доступное пространство. При всей эквивалентности матричной и волновой формулировок интерпретации их авторов были несовместимы.