Хоакин Наварро - Том 37. Женщины-математики. От Гипатии до Эмми Нётер

Ада не ограничилась простыми вычислениями: при правильной последовательности инструкций машина Бэббиджа могла, например, сочинять музыку. Более того, по словам Ады, «аналитическая машина вышивала алгебраические узоры так же, как станок Жаккара вышивает цветы и листья».

В станке Жаккара с помощью отверстий, проделанных в плоских перфокартах по определенной схеме, указывалось, как именно должны проходить нити, и в итоге на ткани появлялись цветные рисунки. Аналогичным образом можно было хранить инструкции, описывающие вычисления. Один набор перфокарт определял элементарные операции, другой указывал, в каком порядке и когда именно следует эти операции выполнять. Ада даже придумала остроумный способ, который позволял повторно использовать перфокарты, описывающие простые и повторяющиеся операции (говоря современным языком, Ада описала циклы программы). Так родилось понятие подпрограммы.

Ада поняла очень важный момент: машина Бэббиджа может работать не только с простыми конкретными числами, но и с символами. Теперь речь шла о настоящих вычислениях в современном смысле этого слова.

Ада всегда утверждала, что аналитическая машина не способна чудесным образом создать что-либо самостоятельно. Да, она могла поразить воображение, но ее «творческие способности» были ограничены творческими способностями ее создателей. Как гласит пословица, «из пустого ничего нельзя взять», что есть не более чем изложение второго начала термодинамики популярным языком. Ни «Я, робот», ни «Терминатор» в нашей Вселенной существовать не могут.

Станок Жаккара, работающий на перфокартах.

* * *

ЧИСЛА БЕРНУЛЛИ

К сожалению, здесь нам не хватит места, чтобы рассказать о числах Бернулли настолько подробно, как они того заслуживают. Эти числа названы в честь Якоба Бернулли(1654–1705) , который ввел их при изучении сумм n-х степеней mпервых чисел:

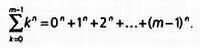
Эта сумма в сокращенном виде записывается так:

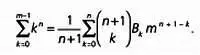
Числа В к, которые всегда будут рациональными, называются числами Бернулли. Первые числа Бернулли таковы:

Их можно вычислить по рекурсивному алгоритму, например с помощью формулы:

Эту формулу можно описать конечной последовательностью действий, или алгоритмом. Именно так поступила Ада Лавлейс: она определила упорядоченную последовательность действий, позволяющих вычислить любое число Бернулли на машине Бэббиджа. Ее беспокоила не эффективность алгоритма, а лишь возможность его выполнения.

Логично, что последовательность чисел Бернулли бесконечна. Нечетные числа Бернулли для n> 2 равны нулю; значения остальных чисел Бернулли хаотичны, и сегодня не существует метода, позволяющего предсказывать их значения. Они тесно связаны с дзета-функцией Римана и считается, что в будущем эти числа сыграют крайне важную роль в теории чисел.

В интернете существуют прекрасные сайты, посвященные числам Бернулли, с помощью которых можно узнать совершенно непостижимые вещи: так, знаменатель несократимой дробной части числа В 10000000 содержит 394815332706046542049668428841497001870 цифр. Это знание может показаться бесполезным, но никогда не знаешь, что и когда может пригодиться.

* * *

ЯЗЫКИ, ПРОГРАММЫ И ПОДПРОГРАММЫ

Первое, что необходимо вычислительной машине, чтобы начать работу, — это понять, чего хочет пользователь. Эта задача решается с помощью языков программирования, которые, разумеется, изобрела не Ада Лавлейс. Далее необходимо схематично описать и упорядочить инструкции так, чтобы считывающие устройства машины могли последовательно считать их. После того как мы зададим начальные условия с помощью набора переменных, машина сможет работать самостоятельно. Если мы изменим начальные значения переменных, то, в общем случае, результат работы машины также изменится. Вычисления будут отличаться, однако описывающие их инструкции останутся неизменными. Одно и то же множество инструкций позволяет выполнить множество вычислений. Эти инструкции представляют собой элементарную программу. Именно программы почти что изобрела Ада (другие считают, что Бэббидж опередил ее на несколько лет) и применила свое изобретение для вычисления чисел Бернулли.

В рамках программы могут быть выделены подпрограммы — фрагменты, которые описывают повторно выполняемые операции и используются множество раз. Они могут храниться в ячейках памяти, и к ним можно обращаться по мере необходимости.

Если гипотетическая вычислительная машина выполняет умножение, то полный алгоритм умножения будет программой, а таблица умножения, например, на 3 — подпрограммой.

Неполный фрагмент аналитической машины Бэббиджа.

* * *

Возможно, пришло время разрушить не слишком реалистичный образ романтичной графини, увлекавшейся математикой. Личная жизнь Ады была достаточно типичной для графини викторианской эпохи: она любила спектакли и танцы, была несколько равнодушна к детям, а порой и к супружескому долгу, коллекционировала украшения и держала множество собак. Ада наверняка страдала какой-то разновидностью биполярного расстройства, так как периоды маниакальной гиперактивности чередовались у нее с приступами депрессии.

Среди друзей графини и тех, с кем она состояла в переписке, были Чарльз Диккенс, Чарльз Уитстон (известный специалист по электричеству), Дэвид Брюстер (изобретатель калейдоскопа) и Майкл Фарадей. С годами она познала искусство кокетства и наверняка имела нескольких поклонников: ее муж позднее уничтожил свыше ста писем, которые счел неподобающими. Вместе с Бэббиджем она открыла для себя очарование ставок на бегах и даже, отчасти сама того не осознавая, связалась с профессиональными игроками, в частности с неким Джоном Кроссом. Они впутали графиню в свои темные дела, и Ада оказалась в долгах. Ее можно по праву вслед за Бэббиджем назвать повелительницей чисел, но стоит заметить, что после смерти она оставила долгов по ставкам на 2 тысячи фунтов.