Анатолий Фоменко - Истину можно вычислить.

Сформулированный выше принцип малых искажений означает, что на практике «в среднем» летописцы ошибались все-таки незначительно, то есть не очень сильно искажали реальные числовые данные.

Обсудим теперь ошибки, которые чаще всего делали летописцы при вычислении длительностей правлений древних царей. Эти три типа ошибок были выделены нами при обработке большого числа конкретных исторических текстов. Выяснилось, что именно эти ошибки чаще всего приводили к искажению реальных длительностей правлений царей.

Ошибка первая.Перестановка, путаница двух соседних царей.

Ошибка вторая.Замена двух царей одним, длительность правления которого равна сумме длительностей их правлений.

Ошибка третья.Неточность в вычислении длительности правления царя. Чем больше эта длительность, тем бóльшую ошибку обычно допускал летописец при ее определении.

Эти три типа ошибок можно описать и смоделировать математически. Начнем с ошибок (1) и (2). Рассмотрим какую-либо династию p = (р 1, р 2, …, р k) из множества D. Вектор q = (q 1, q 2, …, q k) мы назовем ВИРТУАЛЬНОЙ ВАРИАЦИЕЙ вектора (династии) p и будем обозначать его через q = vir(р), если каждая координата q iвектора q получается из координат вектора p одной из следующих двух процедур (1) и (2).

(1) Либо q i= p i(то есть координата не меняется), либо pi переставляется с p i-1, либо p iпереставляется с p i+1, то есть с одной из «соседних координат» вектора p.

(2) Либо q i= p i, либо q iсовпадает с числом p i+ p i+1.

Ясно, что каждый такой вектор (династия) q можно рассматривать как летописную династию, получившуюся из реальной династии p в результате «ее размножения» под воздействием ошибок (1) и (2) летописцев. Другими словами, мы берем каждую реальную династию p = (р 1, р 2, …, p k) из списка D и применяем к ней «возмущения» (1) и (2). То есть либо мы меняем местами два соседних числа p iи p i+1, либо заменяем какое-то число p iсуммой p i+ p i+1или суммой p i-1+ p i. Для каждого номера i мы применяем указанные операции только по одному разу, то есть не рассматриваем «длинные итерации» операций на одном и том же месте i. В результате из одной династии p получается некоторое число виртуальных династий q = vir(р). Количество таких виртуальных династий легко подсчитать.

Таким образом, каждая «точка» из множества D «размножается» и порождает некоторое множество «виртуальных точек», ее окружающих, так сказать, порождает «окрестное облако», «шаровое скопление», рис. 16. Некоторые из получившихся виртуальных династий могут встретиться нам в какой-то конкретной летописи (в этом случае они будут летописными династиями), некоторые остаются всего лишь «теоретически возможными», то есть «виртуальными».

Рис. 16. Каждая династия p порождает некоторое множество vir(p) виртуальных династий. Геометрически они изображаются в виде «облака», «шарового скопления», окружающего точку p в пространстве.

Объединяя все виртуальные династии, получающиеся из всех реальных династий p, составляющих наш список династий D, мы получаем некоторое множество vir(D), то есть «окутывающее облако» исходного множества династий D.

Таким образом, для каждой реальной династии M множество изображающих ее летописных династий можно представлять себе как «шаровое скопление» vir(M). Пусть теперь даны две реальные династии M и N. Если сформулированный нами принцип малых искажений верен, то шаровые скопления vir(M) и vir(N), отвечающие двум заведомо независимым, разным реальным династиям M и N, не пересекаются в пространстве R k. То есть они должны быть расположены достаточно далеко друг от друга рис. 17.

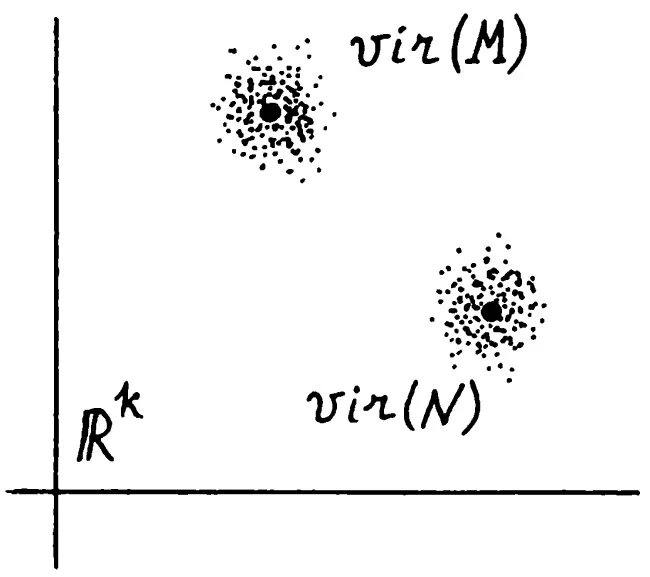
Рис. 17. «Шаровые скопления» vir(M) и vir(N), отвечающие двум заведомо независимым, разным реальным династиям M и N, расположены далеко друг от друга.

Пусть теперь а и b — две какие-то династии из множества vir(D), например, две летописные династии, рис. 18. Мы хотим ввести некоторую количественную меру близости между двумя династиями, то есть «измерить расстояние между ними», оценить, насколько они далеки друг от друга. Простейший способ был бы таким. Рассматривая обе династии как векторы в пространстве R k, можно было бы просто взять евклидово расстояние между ними, то есть подсчитать число r(а, b), квадрат которого имеет вид

(а 1— b 1) 2+ … + (a k— b k) 2.

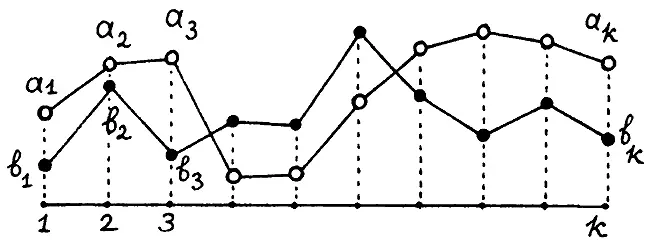
Рис. 18. Наглядное изображение длительностей правлений в двух династиях а и b в виде графиков.

Однако численные эксперименты с конкретными летописными династиями показывают, что это расстояние не позволяет уверенно отделить друг от друга зависимые и независимые пары династий. Другими словами, такие расстояния между заведомо зависимыми летописными династиями и расстояния между заведомо независимыми летописными династиями в некоторых случаях оказываются сравнимыми друг с другом. Оказывается, иногда они имеют «один и тот же порядок».

Тем более нельзя определять «похожесть» или «непохожесть» двух династий, точнее, графиков их правлений, «на глаз». Визуальная похожесть двух графиков может ни о чем не говорить. Можно привести примеры заведомо независимых династий, графики правлений которых окажутся «весьма похожими». И, тем не менее, никакой зависимости тут на самом деле не будет. Как выяснилось, в данной проблеме визуальная близость может легко ввести в заблуждение. Требуется надежная количественная оценка, устраняющая зыбкие субъективные соображения вроде «похожи», «не похожи».

Итак, задача состоит в том, чтобы выяснить, существует ли вообще такая естественная мера близости на множестве всех виртуальных династий, которая позволила бы уверенно отделить зависимые династии от независимых. То есть чтобы «расстояние» между заведомо зависимыми династиями было «мало», а «расстояние» между заведомо независимыми династиями было «велико». Причем требуется, чтобы эти «малые» и «большие» значения существенно отличались бы друг от друга, например, чтобы они были отделены одним или несколькими порядками.

Оказывается, такая мера близости, то есть «расстояние между династиями», действительно существует. К описанию такого коэффициента с(а, b) мы сейчас и перейдем.

Итак, мы построили в пространстве R 15некоторое множество династий D. Были смоделированы две наиболее типичные ошибки, делавшиеся летописцами. Каждая династия из множества D была подвергнута возмущениям типов (1) и (2). При этом каждая точка из D размножилась в несколько точек, что привело к увеличению множества. Получившееся множество мы обозначали через vir(D). Оказалось, что множество vir(D) состоит примерно из 15 × 10 11точек.