Барбара Оакли - Думай как математик: Как решать любые задачи быстрее и эффективнее

ВАША ПОПЫТКА!

Понимание иллюзии компетентности

Анаграммы — это способ перестановки букв в слове или предложении с целью получить другое слово или предложение. Например, у вас есть фраза «Me, radium ace». Можете ли вы переставить буквы так, чтобы они составили фамилию знаменитого физика? [17] Это может оказаться не так-то просто. Однако если бы вы увидели решение здесь же, на этой странице, то от ощущения «Эврика!» подумали бы, будто способность разгадывать анаграммы у вас развита сильнее, чем на самом деле. Аналогичным образом студенты часто ошибочно полагают, будто они выучивают предмет, просто пробегая глазами текст учебника. Из-за того, что решение им уже дано , у них возникает иллюзия компетентности [18].

Найдите в своих записях или в учебнике математическое или естественно-научное понятие. Прочтите о нем, затем отведите взгляд от текста и попробуйте восстановить в памяти прочитанное, одновременно пытаясь лучше его понять. Затем вновь взгляните на текст, перечитайте материал и попытайтесь еще раз восстановить его в памяти. В результате вы удивитесь, насколько это простое упражнение помогает лучше понимать материал.

Чем объемистее ваша мыслительная «библиотека» порций информации, тем легче вам будет решать задачи. Кроме того, с обретением опыта по формированию порций вы начнете замечать, что порции увеличиваются — «ленты» становятся все длиннее.

Вы, возможно, сейчас подумали, что в одной главе учебника по математике или естественным наукам столько понятий и задач, что все их усвоить просто невозможно! И здесь вступает в дело «закон озарений»: удача благоволит к тем, кто прилагает усилия и стремится к цели[23]. Просто попытайтесь сосредоточиться на том, что изучаете. Вы обнаружите, что, когда любое первое понятие или задача попадает в вашу мыслительную библиотеку, второе понятие или задача дается чуть легче. А третье — еще легче. Не то чтобы процесс идет совершенно без усилий, но он упрощается.

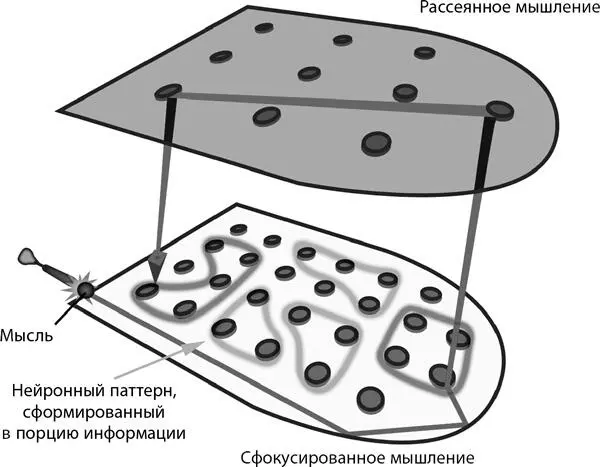
Если ваша библиотека понятий и решений уже существует в виде порционных шаблонов, вы можете легко «перескочить» к нужному решению задачи — необходимо лишь прислушаться к внутреннему голосу, который шепотом подает вам советы из рассеянного состояния. Рассеянный режим также помогает соединить две или три порции информации нестандартным, еще не применявшимся способом, что помогает при решении нетривиальных задач. Решать задачи можно двумя путями: первый — постепенные пошаговые рассуждения, второй — цельная, нерасчленимая интуиция. Последовательное мышление, при котором каждый малый шаг направлен к решению, связано со сфокусированным режимом. Интуиция же часто считается связанной с творческим, рассеянным режимом, при котором объединяются несколько разрозненных идей. Самые сложные задачи решаются с помощью интуиции, поскольку они требуют отхода от уже известных путей [24]. Не забудьте, что полуслучайный способ связывания идей, который свойствен рассеянному состоянию, требует тщательной проверки решения в сфокусированном состоянии. Интуитивные озарения не всегда верны! [25]

Когда вы создаете библиотеку сформированных порций информации, вы учите мозг распознавать не только конкретную задачу, но и разные типы и классы задач, так что со временем вы будете автоматически видеть способы, предпочтительные для решения тех задач, которые вам встретятся. Вы начнете видеть закономерности, облегчающие поиск решения, и вскоре поймете, как много различных решений маячит в отдаленных уголках памяти. А перед экзаменами такие знания будет легко упорядочить, чтобы иметь наготове нужные решения.

ВАША ПОПЫТКА!

Не понимаю! Что делать?

Если вы не понимаете метод, которому вас учат, то остановитесь и попробуйте вернуться назад. Зайдите в Интернет и выясните, кто первым предложил этот способ или кто раньше его использовал. Попытайтесь понять, каким образом первооткрыватель метода пришел к такой идее и почему этот прием до сих пор применяется, — так вы можете наткнуться на простое объяснение, которое даст вам необходимую информацию о том, почему этому методу решения учат студентов и зачем он вам может понадобиться.

Практика — путь к надежным знаниям

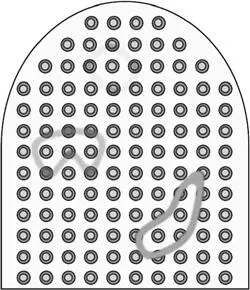
Я уже упоминала, что простого понимания принципа обычно недостаточно для формирования порции информации. Схематическое изображение мозга поможет вам лучше это понять. Порции (замкнутые петли) на рисунке — всего лишь расширенные следы памяти, которые появились из-за того, что вы связали воедино факты и достигли понимания. Порция информации, стало быть, — это просто более сложный вид следов памяти. В верхней части рисунка — слабая порция, которая начинает формироваться после того, как вы поняли материал и раз-другой в нем попрактиковались. В центре линия темнее: это более мощный нейронный паттерн, появившийся после более обширной практики и применения порции к разным контекстам. Внизу — самая темная порция, надежно укорененная в долговременной памяти.

Кстати, очень важно закрепить изначальный паттерн через день после формирования, иначе он может быстро стереться (о важности периодических повторений мы поговорим позже). А если решать однотипные задачи одним и тем же неправильным способом, то в памяти отпечатается неверный процесс. Вот почему так необходимо перепроверять то, что вы делаете. Даже верный ответ может временами увести вас в ненужную сторону, если он получен в результате некорректной процедуры.

Решение математических и естественно-научных задач похоже на исполнение фортепианной пьесы. Чем больше практикуетесь, тем надежнее, четче и сильнее становятся ментальные паттерны.

О важности формирования порций

«Математика порой оказывается удивительно компактной: вы можете долго, шаг за шагом биться над задачей, подходить к идее или процессу с разных сторон, но, как только пришло понимание и вы увидели масштаб явления на фоне целого, материал становится более компактным: вы можете его отложить в сторону, при необходимости вспомнить его быстро и в полном объеме, использовать его как рядовой этап в других мыслительных процессах. То озарение, которое приходит вместе с таким “сжатием” материала до компактного, и составляет одну из главных радостей изучения математики» [26].

Уильям Терстон, лауреат Филдсовской премии (высшей награды в математике)