Леонид Букин - Статистика: учебное пособие

При изучении экономических явлений статистика встречается с разнообразной вариацией признаков, характеризующих отдельные единицы совокупностей. Величины признаков варьируют под воздействием различных причин и условий. Чем разнообразнее условия, влияющие на размер признака, тем больше его вариация.

Рассмотренные показатели центральной тенденции и показатели вариации представляют собой частные случаи некоторой единой системы статистических характеристик распределения. Такая единая система характеристик может быть представлена моментами статистического распределения. Если при вычислении моментов за произвольную постоянную принимается средняя арифметическая, то такие моменты называются центральными.

Общая формула центральных моментов k-го порядка имеет вид:

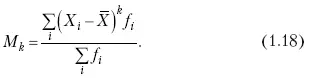
Иначе говоря, центральные моменты k-го порядка представляют собой среднюю арифметическую из k – x степеней отклонений значений признака от средней арифметической.

1. Центральный момент нулевого порядка равен единице при k = 0:

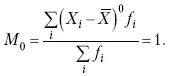
2. Центральный момент первого порядка равен нулю при k = 1:

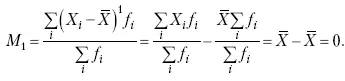
3. Центральный момент второго порядка представляет собой дисперсию данного распределения при k = 2:

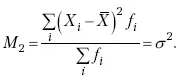
4. Центральный момент третьего порядка имеет вид:

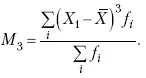
Если распределение симметричное, то нетрудно видеть, что центральный момент третьего порядка равен нулю, так как минусовые отклонения ( X i – X ) 3в левой ветви распределения будут уравновешиваться положительными отклонениями в правой части. Такое взаимное погашение отклонений в симметричных рядах распределения сохраняет силу для всех нечетных центральных моментов.

Конец ознакомительного фрагмента.