А. Болотова - Развитие познавательной самостоятельности младших школьников в процессе обучения математике с использованием рабочих тетрадей

Развитие познавательной самостоятельности может осуществляться преимущественно в рамках обучения конкретному предмету. Среди предметов школьной программы, изучаемых в младших классах, изучение математики, по нашему мнению, наиболее благоприятствует развитию познавательной самостоятельности, так как поиск решения математических задач требует, прежде всего, самостоятельной мыслительной деятельности для построения плана решения, самопроверки полученного результата, умений самостоятельно пользоваться правилами и алгоритмами, а также умений применять систему обобщенных знаний. Математическая деятельность при изучении математики в начальной школе заключается, прежде всего, в создании детьми моделей наблюдаемых фрагментов реальности. Обучение построению математических моделей реальных, доступных наблюдению детей явлений обеспечивает понимание сложных взаимосвязей математического знания, его содержательных аспектов.

В решении проблемы развития познавательной самостоятельности младших школьников на уроках математики эффективным средством является рабочая тетрадь.

Модернизация образования, затронув все сферы образовательного процесса, коснулась и средств обучения. Изменение целей образования влечет за собой преобразование содержания, средств и методов обучения, требует пересмотра всего учебно-методического комплекса, в том числе и входящих в его состав рабочих тетрадей для школьников.

Рабочая тетрадь является специфическим средством развития познавательной активности учащихся. Основные дидактические функции рабочих тетрадей заключаются в следующем: повышение степени наглядности, доступности для учащихся учебного материала, в максимальной степени развитие познавательной деятельности учащихся, интенсификация труда учащихся.

Какой должна быть рабочая тетрадь по математике для начальной школы, если одной из целей будет развитие познавательной самостоятельности? В основе структуры рабочей тетради, направленной на развитие познавательной самостоятельности при обучении математике в младших классах положены следующие принципы: принцип визуализации математических понятий, принцип согласования обучения математике с ходом ее познания ребенком, принцип учета базовых механизмов интеллектуальной деятельности (И. В. Шадрина).Визуализация математических понятий позволяет эффективно организовать самостоятельную познавательную деятельность детей, сформировать образы математических понятий наиболее доступным для них способом, самостоятельно их конструируя и преобразовывая. Согласование обучения математике с ходом ее познания ребенком предполагает учет познавательных особенностей младших школьников. Реализация принципа учета базовых механизмов интеллектуальной деятельности означает, что проблемная ситуация анализируется в предметной форме, описывается вербально, строится обобщенная графическая модель, осуществляется ее перевод на знаково-символический язык.

В структуре листа рабочей тетради отражено поэтапное построение моделей рассматриваемой ситуации.

Таблица 1.

Структура листа рабочей тетради

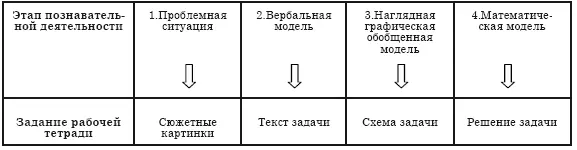
Способы предъявления заданий в рабочей тетради должны отвечать следующим условиям:

• направленность на самостоятельный поиск решения задачи;

• опора на наглядно-образное представление математической информации;

• использование моделей рассматриваемых ситуаций разного уровня обобщенности;

• задания каждого листа рабочей тетради структурированы так, что ведут к разрешению одной проблемной ситуации.

В данном пособии приводятся методические разработки уроков математики в начальной школе с использованием рабочих тетрадей, направленных на развитие познавательной самостоятельности.

Рассмотри картинку. Расставь игрушки в другом порядке.

Рис. 1

Учитель: Какие предметы изображены?

Ученик: Игрушки. Мяч, юла, матрешка.

Учитель: Чем отличаются картинки? Чем похожи картинки?

Ученик: Игрушки на картинках одинаковые. Игрушки на второй картинке стоят в другом порядке.

Учитель: Что требуется сделать с игрушками?

Ученик: Поставить игрушки в другом порядке.

Учитель: Какая игрушка следует за мячиком?

Ученик: За мячиком следует матрешка.

Учитель: Какая игрушка находится между мячиком и юлой?

Ученик: Матрешка находится между мячиком и юлой.

Учитель: Какая игрушка следует за матрешкой?

Ученик: Сразу за матрешкой следует юла. Так же подробно проговаривая, анализируется и расположение игрушек на второй картинке.

Учитель: Попробуйте с помощью карточек показать на доске, как можно расположить игрушки по-другому.

Несколько учеников предлагают, как можно расположить игрушки, выкладывают их последовательность на доске. Остальные дети проверяют, сравнивая новую последовательность с теми, которые нарисованы на листах.

Ученик: Я расставил так. Сначала мячик, за мячиком следует юла, за юлой следует матрешка.

Степень самостоятельности при таком виде работы невелика, однако учитель вовлекает в работу как можно больше детей, задает вопросы, предлагает работу с карточками.

Учитель: А теперь по желанию нарисуйте на свободной строке игрушки в таком порядке, чтобы он отличался от порядка на первой и на второй картинке. Таким образом, учитель предлагает ребенку самостоятельно сделать выбор и попробовать использовать полученные знания. Дети меняются листами и сравнивают последовательности.

Рис. 2

Справа на рисунке приведены примеры того, какие последовательности игрушек рисовали ученики.

Раскрась кольца пирамидки, если желтое кольцо находится между красным и синим кольцами, а синее – между желтым и зеленым.

Рис. 3

У учителя на доске нарисована такая же пирамидка.

Учитель: Что изображено на картинке?

Ученик: Пирамидка.