Журнал «Юный техник» - Юный техник, 2006 № 11

7. Тело кубической формы находится под водой в открытом водоеме так, что грань куба параллельна поверхности воды и находится на глубине h 1 = 2 м. Сила F 1, действующая на нижнюю грань куба со стороны воды, в 1,1 раза больше силы F 2 , действующей на верхнюю грань. Найдите длину ребра куба, а также F 1 и F 2 . Атмосферное давление Р 0 равно 10 5Па.

8. Энергия солнечного излучения, падающего в секунду на один квадратный метр земной поверхности, составляет примерно 1000 Дж. На сколько уменьшится толщина льдины на поверхности замерзшего водоема за один световой день? Считать, что лед поглощает 10 % падающего излучения. Температуру льда принять равной 0 °C, а продолжительность светового дня — 6 часов.

9. Смешивают m 1 = 300 г воды при температуре t 1 = 10 °C и m 2 = 400 г льда при температуре t 2 = -20 °C. Определить установившуюся температуру смеси. Удельная теплоемкость воды с в = 4200 Дж/(кг∙К), льда с л = 2100 Дж/(кг∙К), удельная теплота плавления льда λ = 330∙10 3Дж/кг. Потерями теплоты пренебречь.

10. Для нормальной работы некоторого электрического прибора требуется, чтобы подаваемое на него напряжение было не менее U мин = 200 В. В этом случае потребляемая прибором мощность равна N = 1 кВт. В силу большой удаленности прибора от розетки, его приходится включать в сеть через удлинитель. Напряжение в розетке составляет U = 220 В. На каком максимальном l удалении от розетки может работать прибор, если провода удлинителя изготовлены из меди и имеют диаметр 1 мм?

11. Расстояние S = 18 км между двумя станциями поезд проходит со средней скоростью V cр = 54 км/ч, причем на разгон тратит t 1 = 2 мин, затем идет с постоянной скоростью и на замедление до полной остановки тратит t 2 = 1 мин. Определите наибольшую скорость поезда. Разгон и торможение происходят равноускоренно.

12. Расстояние между двумя свободно падающими каплями через время t 1 = 2 с после начала падения второй капли было L = 25 м. На сколько позднее начала падать вторая капля? Сопротивление воздуха не учитывать. Капли падают из одной точки.

13. Небольшой груз массой m лежит на длинной доске массой М (рис. 2).

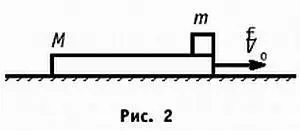
Коэффициент трения между доской и грузом равен μ 1 , а между доской и столом — μ 2 . По доске наносят удар, и она начинает двигаться поступательно со скоростью V 0 по поверхности стола. Определить время, через которое прекратится скольжение груза по доске.

14. Мяч массой m = 5 кг бросают со скоростью V 0 = 10 м/с под углом α = 30° к горизонту. Затем мяч сталкивается с вертикальной стенкой и после упругого удара возвращается в точку броска. Найдите среднюю силу, действующую на мяч со стороны стены, если длительность удара составляет τ = 0,01 с. Сопротивление воздуха не учитывать.

15. Один моль гелия нагревается при постоянном объеме V 0 = 400 л так, что относительное увеличение его давления составило Р/Р 0 = 0,004 (здесь Р 0 — начальное давление гелия). На сколько градусов Т увеличилась температура газа, если его начальная температура равна Т 0 = 500 К?

16. В цилиндре под поршнем площадью S = 100 см 2находится азот (N 2) массой m a = 560 г. В цилиндр вводится водород (Н 2) массой m в = 1 г, и поршень поднимается. Чтобы вернуть объем смеси газов под поршнем к прежнему значению, на поршень кладут груз некоторой массы m . Определите m , если известно, что масса поршня М = 100 кг, атмосферное давление P о = 10 5Па. Температура в цилиндре поддерживается постоянной.

17. Три одинаковых заряженных шарика связаны легкими непроводящими нитями одинаковой длины l и находятся в покое на гладкой горизонтальной поверхности (см. рис. 3).

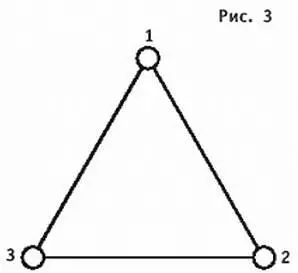
Массы шариков одинаковы и равны m . Заряды шариков одинаковы и равны q . Две нити одновременно пережигают. Найти модули ускорений всех шариков сразу после пережигания нитей.

(После порядкового номера задачи в скобках указано количество очков за задачу.)

1(4).Студент купил принтер, клавиатуру и мышку, потратив 5970 рублей 75 копеек. Известно, что стоимость мышки составляет 1/3 стоимости клавиатуры, а стоимость клавиатуры и мышки, вместе взятых, — 4/21 стоимости принтера. Сколько стоит каждый предмет в отдельности?

2(5).Свежий виноград имеет влажность 99 %. Через месяц после сбора ягод влажность составляет уже 98 %. Определите, на сколько процентов изменилась масса винограда.

3(6). а) На сколько градусов поворачивается за минуту минутная стрелка? Часовая стрелка?

б) В полдень минутная и часовая стрелки совпали. Когда они совпадут в следующий раз?

в) Какой угол образуют минутная и часовая стрелки в 3 часа 5 минут?

4(5). — Спускаясь вниз по эскалатору, я насчитал 50 ступенек, — сказал волк.

— А я насчитал 75, — возразил заяц, — но я спускался в три раза быстрее.

Если бы эскалатор остановился, то сколько ступенек можно было бы насчитать на его видимой части? Предполагается, что волк и заяц двигались равномерно и скорость эскалатора постоянна.

5(6).Угол при вершине В равнобедренного треугольника ABC равен 108°. Перпендикуляр к биссектрисе AD этого треугольника, проходящий через точку D , пересекает сторону АС в точке Е . Найдите DE , если DB = 6.

6(5).Найдите число, при делении на которое три числа 480 608, 508 811 и 723 217 давали бы один и тот же остаток.

7(6).Решите уравнение:

5/(х — 1) + 3/(х — 2) + 3/(х — 3) +5/(х — 4) = 0.

8(5).Решите неравенство:

9(8).Окружность, построенная на большем основании трапеции как на диаметре, проходит через середины боковых сторон и касается меньшего основания. Найдите углы трапеции.

10(8). а) Изобразите на плоскости множество точек, координаты которых удовлетворяют условию:

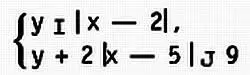
б) Найдите площадь полученной фигуры.

11(7).На продолжениях сторон АВ, ВС, CD и DA и выпуклого четырехугольника ABCD соответственно за точки В, С, D и А отложены отрезки ВВ 1, CC 1, DD 1 и АА 1 , равные этим сторонам. Найдите площадь четырехугольника A 1B 1C 1D 1 , если площадь четырехугольника ABCD равна 5.