Журнал «Юный техник» - Юный техник, 2003 № 11

9. Фамилия, имя, отчество преподавателей

по физике Еремин Владимир Александрович

по математике Михайлова Елена Игоревна

10. Каким образом к Вам попала эта афиша?

В ЗФТШ ежегодно приходит более 5 тысяч вступительных работ. Пожалуйста, обратите внимание на правильность заполнения анкеты! Пишите аккуратно, лучше печатными буквами.

ВНИМАНИЕ!Для получения ответа на вступительное задание и для отправки вам первых заданий обязательно вложите в тетрадь два одинаковых бандерольных конверта размером 160x230 с наклеенными марками достоинством 7 руб. На конвертах четко напишите свой домашний адрес. Ученикам, зачисленным в ЗФТШ в рамках утвержденного плана приема, необходимо будет оплатить безвозмездный целевой взнос на ведение уставной деятельности школы. Сумма взноса будет составлять ориентировочно для учащихся заочного и очного отделений 300–500 руб. в год, для очно-заочного — 600 — 1000 руб. (с каждой факультативной группы).

Срок отправки решения — не позднее 1 марта 2004 года. Вступительные работы обратно не высылаются. Решение приемной комиссии будет сообщено не позднее 1 августа 2004 года.

Тетрадь с выполненными заданиями (по физике и математике) высылайте по адресу: 141700, г. Долгопрудный Московской области, Институтский пер., 9, ЗФТШ при МФТИ.

Ниже приводятся вступительные задания по физике и математике. В задании по физике: задачи 1–5 предназначены для учащихся седьмых классов: 1, 3, 4, 8, 9, 11 — для восьмых классов; 1, 3, 5, 6, 8, 9, 11 — для учащихся девятых классов; задачи 5–8, 10–12 — для учащихся десятых классов. В задании по математике: задачи 1–5 для учащихся седьмых классов; 2–7 — для восьмых классов; 5 — 11 — для девятых классов; 8 — 14 — для десятых классов.

Номера классов указаны на текущий 2003–2004 учебный год.

1. Влажность свежескошенной травы 60 %, сена — 15 %. Сколько сена получится из одной тонны свежескошенной травы?

2. Найти все такие натуральные числа, которые увеличиваются в 9 раз, если между цифрой единиц и цифрой десятков вставить нуль.

3. В треугольнике ABC проведена медиана АК . Найдите величину угла А, если известно, что АК = ВК .

4. Два грузовика одновременно вышли из А в В . Первый грузовик половину времени, затраченного им на весь путь, шел со скоростью 50 км/ч, а остальную часть времени шел со скоростью 40 км/ч. Второй грузовик первую половину пути шел со скоростью 40 км/ч, а вторую — со скоростью 50 км/ч. Какой из этих грузовиков раньше прибыл в В.

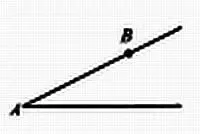
5. Дан угол А и точка В на одной из сторон угла. Найдите на другой стороне угла точку С такую, что сумма отрезков ВА и ВС равна заданному отрезку а .

6. Найдите все значения параметра а , при которых система уравнений

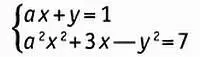
не имеет решений.

7. В треугольнике ABC (с тупым углом В) проведены высоты AD и BE. Найдите углы треугольника DEC, если известно, что L BAD = 15°, L АВЕ = 20°.

8. Числа a 1'a 2'a 3'образуют арифметическую прогрессию, а квадраты этих чисел составляют геометрическую прогрессию. Найдите a 1'a 2'a 3'если известно, что a 1+ a 2+ a 3= 21.

9. В вазе лежат конфеты двух сортов, причем число конфет первого сорта более чем на 20 штук превышает число конфет второго сорта. Одна конфета первого сорта весит 2 г, а конфета второго сорта — 3 г. Из вазы взяли 15 конфет одного сорта, вес которых составил 1/ 5часть от веса всех конфет, лежавших в вазе. Затем было взято еще 20 конфет другого сорта; их вес оказался равным весу оставшихся в вазе конфет. Сколько конфет каждого сорта лежало первоначально в вазе?

10. В трапеции MNPQ ( MQ II NP ) угол NPM в два раза больше угла NQM. NP = MP = 13/2, MQ = 12. Найдите площадь трапеции.

11. Для каждого значения параметра о решите неравенство

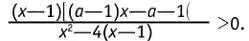
Найдите все значения параметра а, при которых данное неравенство равносильно неравенству

х 4+ 3 > 4х(1 — х + х 2).

12. Длина медианы остроугольного треугольника ABC, которая проведена к его стороне длиной 6 см, равна 5 см. Найдите площадь треугольника ABC , если величины его углов А и В связаны соотношением

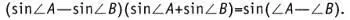
13. Для каждого значения параметра а решите систему уравнений

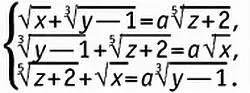
14. Решите уравнение

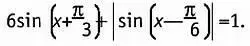
1. Две дороги пересекаются перпендикулярно одна другой. По первой дороге по направлению к перекрестку едет машина со скоростью 60 км/ч, а по второй — трактор со скоростью 25 км/ч. Через какое время после встречи на перекрестке расстояние между машиной и трактором станет равным 6,5 км?

2. По дороге в горку трамвай ехал со скоростью 40 км/ч, а возвращаясь обратно по той же дороге с горки — 60 км/ч. Чему была равна средняя скорость трамвая? Указание: здесь речь идет о средней скорости, равной отношению пройденного пути ко времени.

3. В высокой узкой U-образной вертикальной пробирке с постоянным поперечным сечением находится вода. В левое колено аккуратно наливают керосин. На какую величину различаются уровни свободной поверхности жидкостей в коленах? Высота столба керосина в левом колене равна 10 см. Плотность воды 1000 кг/м 3, керосина — 800 кг/м 3.

4. К воздушному шарику объемом 2 л привязаны такие грузы, что окруженный со всех сторон водой шарик свободно плавает в воде на некоторой глубине, находясь в неустойчивом равновесии. Через некоторое время часть воздуха вышла, и объем шарика уменьшился вдвое. Груз какой массы нужно снять с шарика, чтобы он остался плавать на той же глубине, что и раньше? Массой воздуха в шарике пренебречь, массой оболочки не пренебрегать. Плотность материала грузов в три раза больше плотности воды.

5. Деревянная деталь плавает в воде, погрузившись в воду на 2/3 своего объема. Как изменится архимедова сила, действующая на деталь, если ее поместить в керосин? Какую минимальную силу нужно будет приложить, чтобы полностью «утопить» деталь в керосине? Плотность воды 1000 кг/м 3, керосина — 800 кг/м 3, масса детали 400 г.