Шон Кэрролл - Вечность. В поисках окончательной теории времени

Вспомним снова шахматные доски. На событие, происходившее в определенный момент времени, влияло событие, происшедшее моментом ранее. Но то, что происходило в определенной точке «пространства» (совокупности клеток в пределах одной строки), никак не было связано с происходящим в любой другой точке пространства в тот же момент времени. В любой конкретной строке у нас могло быть абсолютно любое распределение белых и серых квадратиков. Никаких правил типа «если здесь находится серая клетка, то через двадцать мест направо должна находиться белая» не существовало. Да, по ходу времени клетки «взаимодействовали» друг с другом, но взаимодействие всегда ограничивалось соседними клетками. Схожим образом, в реальном мире объекты сталкиваются друг с другом и воздействуют на другие объекты, находящиеся поблизости, но не где-то далеко. Это локальность.

Локальность приводит к важному следствию для энтропии. Возьмем, как обычно, контейнер с газом и подсчитаем энтропию газа в контейнере. Теперь мысленно поделим контейнер на две части и вычислим энтропию в каждой половине. (Не нужно воображать физический барьер, просто рассматривайте левую и правую половины контейнера по отдельности.) Как связаны между собой полная энтропия контейнера и энтропии двух половин, взятые отдельно?

Ответ таков: энтропию целого контейнера можно получить, просто сложив энтропию одной его половины с энтропией другой его половины. Казалось бы, это непосредственно следует из определения энтропии по Больцману – собственно, поэтому в данном определении и присутствует логарифм. У нас есть определенное количество допустимых микросостояний в одной половине контейнера и определенное количество допустимых микросостояний в другой. Общее количество микросостояний рассчитывается так: для каждого возможного микросостояния левой половины мы можем выбрать любое из возможных состояний правой половины. Таким образом, мы получаем общее количество микросостояний путем умножения числа микросостояний слева на число микросостояний справа. Но энтропия – это логарифм полученного значения, а логарифм « X умноженного на Y » равен «логарифм X » плюс «логарифм Y ».

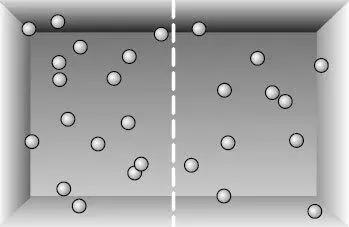
Рис. 12.6.Контейнер с газом, мысленно поделенный на две половины. Полная энтропия содержимого контейнера равна сумме энтропий двух половин содержимого

Итак, энтропия всего контейнера равна простой сумме энтропий двух половин. И это правило будет работать независимо от того, каким образом мы разделим исходный контейнер и на сколько частей; полная энтропия системы всегда равна сумме энтропий подсистем. Это означает, что максимальная возможная для выбранного контейнера энтропия всегда будет пропорциональна его объему : чем больше у нас пространства, тем большее значение может принимать энтропия, так что она естественным образом масштабируется с увеличением объема.

Однако обратите внимание на коварное предположение, присутствующее в этом рассуждении: мы подсчитали количество состояний в одной половине контейнера, а затем умножили его на количество состояний в другой половине. Другими словами, предполагалось, что то, что происходило в одной половине контейнера, никак не зависело от происходящего в другой его половине. А это как раз предположение о локальности.

Когда на сцену выходит гравитация, все эти доводы рушатся. Гравитация устанавливает верхний предел на энтропию, которую мы можем впихнуть в контейнер, равный энтропии самой большой черной дыры, способной поместиться в данную тару. Однако энтропия черной дыры не пропорциональна заключенному в ней объему – она пропорциональна площади горизонта событий. А площадь может очень сильно отличаться от объема! Если у нас есть сфера диаметром один метр и мы увеличим ее в размере так, чтобы ее диаметр возрос до двух метров, то внутренний объем сферы возрастет в восемь раз (2 3), тогда как площадь ее поверхности возрастет лишь в четыре раза (2 2).

Вывод прост: квантовая гравитация не подчиняется принципу локальности. В квантовой гравитации происходящее здесь не может быть абсолютно независимым от происходящего там. Максимальное количество вещей, которые могут происходить в какой-то области пространства (число возможных микросостояний в ней), не пропорционально объему этой области; оно пропорционально площади поверхности границы данной области. В реальном мире, который описывает квантовая гравитация, в заданную область получается втиснуть намного меньше информации, чем мы могли бы наивно предполагать, не беря в расчет гравитацию.

Эта догадка получила название голографического принципа. Впервые данный принцип был предложен нидерландским ученым, нобелевским лауреатом Герардом 'т Хоофтом и американским физиком-теоретиком, специалистом в области теории струн Леонардом Сасскиндом, а позднее он был формализован немецко-американским физиком Рафаэлем Буссо (бывшим учеником Стивена Хокинга). [232]На первый взгляд голографический принцип может казаться не слишком интересным. Хорошо, число возможных состояний в области пропорционально размеру этой области в квадрате, а не ее размеру в кубе. Но это совсем не тот тип замечаний, которые позволяют привлечь к себе внимание и моментально очаровать незнакомцев на вечеринке.

Вот почему голография важна: этот принцип означает, что пространство – время не фундаментально. Обычно, размышляя о происходящем во Вселенной, мы неявно предполагаем существование чего-то вроде локальности; мы отдельно описываем то, что случилось здесь, и отдельно то, что случилось там, не связывая между собой все возможные положения в пространстве. Голография утверждает, что в принципе так делать нельзя, потому что еле уловимые связи существуют между любыми событиями, происходящими в разных точках пространства, и это здорово ограничивает нашу свободу в описании конфигурации материи в пространстве.

Обычная голограмма создает впечатление объемного изображения за счет отражения света от особой двумерной поверхности. Голографический принцип гласит, что на фундаментальном уровне Вселенная примерно такая же: все, что, по нашему мнению, происходит в трехмерном пространстве, в действительности тайно закодировано на двумерной поверхности, насыщенной информацией. Трехмерное пространство, в котором мы живем и дышим, можно было бы (опять же в принципе) реконструировать, отталкиваясь от намного более компактного описания. Доступ к этому описанию у нас может быть, а может и отсутствовать. Второй вариант намного более вероятен, но в следующем разделе мы детально рассмотрим пример ситуации, когда эта информация нам доступна.