Шон Кэрролл - Вечность. В поисках окончательной теории времени

Базовые единицы измерения, используемые физиками, – это единицы времени, длины и массы; используются также их комбинации. Самый короткий интервал времени, представляющий интерес, – это планковское время, примерно 10 –43секунд. Предположительно инфляция продолжалась около 10 –30секунд или меньше, хотя это значение чрезвычайно неточно. Вселенная создала гелий из протонов и нейтронов где-то через 100 секунд после Большого взрыва, а прозрачной стала в момент рекомбинации, 380 000 лет (10 13секунд) спустя. (В одном году около 3 · 10 7секунды.) Сейчас наблюдаемой Вселенной 14 миллиардов лет (примерно 4 · 10 17секунды). Еще через 10 100лет или около того все черные дыры практически полностью испарятся, оставив после себя холодную и пустую Вселенную.

Самая маленькая длина – это планковская длина, около 10 –33сантиметров. Размер протона – примерно 10 –13сантиметров, а размер человеческого существа – примерно 10 2сантиметров (это очень низкое человеческое существо, но мы сейчас оперируем приблизительными значениями). Расстояние от Земли до Солнца – около 10 13сантиметров; расстояние до ближайшей звезды – около 10 18сантиметров, а размер наблюдаемой Вселенной – около 10 28сантиметров.

Планковская масса – это примерно 10 –5граммов; для отдельной частицы это было бы невероятно много, но по макроскопическим стандартам – совсем нет. Самые легкие частицы с ненулевой массой – нейтрино; мы даже пока не знаем точно, какова их масса, но минимальная вроде бы составляет около 10 –36граммов. Масса протона – приблизительно 10 –24граммов, а человеческого существа – примерно 10 5граммов. Солнце весит около 10 33граммов, галактика – около 10 45граммов, а масса, содержащаяся в пределах наблюдаемой Вселенной, составляет около 10 56граммов. Логарифмы

Логарифмическая функция – самая простая вещь на свете: она всего лишь отменяет показательную функцию. Если у нас есть какое-то число, которое может быть выражено в форме 10 x, а это возможно для любого положительного числа, то логарифм этого числа равен просто [312]

lg(10 x) = x .

Что может быть проще? Точно так же возведение в степень отменяет логарифм:

10 lgx= x .

Можно также думать об этом так: если число представляет собой целую степень десяти (например, 10, 100, 1 000 и т. п.), то логарифм – это просто-напросто число нулей справа от единицы:

lg(10) = 1,

lg(100) = 2,

lg(1000) = 3.

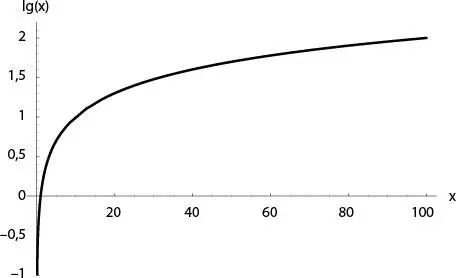
Рис. П2.Логарифмическая функция lg(x). Она не определена для отрицательных значений x, и по мере приближения x к нулю справа значение логарифма стремится к минус бесконечности

Однако так же как и показательная функция, логарифм – это гладкая функция, как показано на рис. П2. Логарифм числа 2,5 равен 0,3979, логарифм 25 равен примерно 1,3979, логарифм 250 – примерно 2,3979 и т. д. Единственное ограничение заключается в том, что невозможно взять логарифм от отрицательного числа, и это разумно, так как логарифм отменяет показательную функцию, а получить отрицательное число в результате операции возведения в степень невозможно. Грубо говоря, для больших чисел логарифм – это просто «количество цифр в числе».

Логарифм демонстрирует свойство, аналогичное тому, с которым мы уже познакомились выше для возведения в степень (результат возведения в степень, равную сумме чисел, равен произведению соответствующих степеней): логарифм произведения равен сумме логарифмов, то есть

log( x · y ) = log( x ) + log( y ).

Это чудесное свойство делает логарифмы невероятно полезными для изучения энтропии. Как мы обсуждали в главе 8, физическое свойство энтропии заключается в том, что энтропия двух систем после объединения равна сумме энтропий этих систем по отдельности. Но число возможных состояний объединенной системы равно произведению количеств возможных состояний двух систем. Поэтому Больцман сделал вывод о том, что энтропия должна быть равна логарифму числа состояний, а не самому числу состояний. В главе 9 мы рассказали схожую историю, но уже для информации: Шэннон хотел найти меру информации, для которой общая информация, переданная в двух независимых сообщениях, была бы равна сумме количеств информации в каждом из сообщений, и он также прибегнул к помощи логарифма.

Проще говоря, логарифмы обладают таким милым свойством, что они берут огромные числа и стачивают их до управляемых размеров. Беря логарифм от такого тяжеловесного числа, как миллиард, мы получаем симпатичную девятку. Логарифм – функция монотонная, то есть его значение всегда увеличивается по мере увеличения значения, от которого берется логарифм. Таким образом, логарифм предоставляет специфическую меру того, насколько число велико, но при этом сжимает громадные числа до разумных размеров, что чрезвычайно полезно в таких областях, как космология, статистическая механика и даже экономика.

В заключение необходимо отметить, что, так же как и степенная функция, логарифмы могут браться по разным основаниям. «Логарифм по основанию b » числа x – это степень, в которую необходимо возвести b , для того чтобы получить x :

log2(2 x) = x ,

log12(12 x) = x

и т. д. Если мы не записываем основание явно, то подразумевается, что оно равно 10, потому что именно таким количеством пальцев обладает большинство людей. Однако ученые и математики частенько используют нечто странное, а именно натуральный логарифм, который часто записывается как ln( x ) и основанием в котором служит число Эйлера:

ln( x ) = loge( x ),

e = 2,7182818284…

Число Эйлера – это иррациональное число, как π или квадратный корень из двух, так что в десятичной записи, которая частично показана выше, оно продолжается бесконечно. На первый взгляд кажется, что использовать нечто подобное в качестве основания логарифма невероятно странно. Но в действительности если углубиться в математику, то выяснится, что число e обладает множеством приятных свойств: в математическом анализе, например, функция ex – единственная (за исключением вырожденной функции, всегда равной нулю), которая равна своей производной, а также интегралу от себя самой. В этой книге все наши логарифмы брались по основанию 10 и обозначались lg, но если вы решите взяться за физику и математику на высшем уровне, то будете постоянно встречаться с натуральными логарифмами.

Благодарности

Для того чтобы выпестовать книгу – от концепции до публикации, необходимо приложить большие коллективные усилия, и я должен поблагодарить множество людей, которые помогали мне на этом пути. В период, когда существовали еще только лишь неясные очертания будущей книги, мне посчастливилось повстречать, полюбить и создать семью с женщиной, которая оказалась невероятно талантливым писателем и популяризатором науки. Я бесконечно благодарен Дженнифер Оллетт (Jennifer Ouellette), благодаря которой эта книга стала несравнимо лучше, а весь процесс обрел смысл.