Питер Робинсон - С ПОЛЯРОИДОМ В АДУ: Как получают МБА

— После 32-кратного складывания, — продолжил Купер, — толщина будет равна двум в 32-й степени, или 4 294 967 296 листов. Умножив это число на 0,004, получаем 17 179 869 дюймов. Семнадцать миллионов сто семьдесят девять тысяч восемьсот шестьдесят девять дюймов составляют собой 1 431 655 футов. А один миллион четыреста тридцать одна тысяча шестьсот пятьдесят пять футов равны примерно 271 миле.

— Дамы и господа, получить правильный ответ интуитивно невозможно. Но зато математика подведет вас к нему через коротенькую серию вычислений.

Даже мне пришлось признать, что Купер-таки продемонстрировал то, чего добивался. Математика в состоянии предоставить компактный, мощный инструмент для анализа. На минуту я даже испытал нечто вроде озарения: лирик, мельком ощутивший поэзию математики. Затем Купер вернулся обратно к учебной программе, начал обсуждать системы совместных линейных уравнений и точно так же совместно, то бишь по ходу дела, оставил меня за кормой.

Нудный труд, перемежаемый краткими, быстротекущими минутами просветления, стал типичной моделью занятий "математического лагеря". Мы прогрызались сквозь линейные уравнения, выписанные в X-Y координатах декартовых диаграмм, через векторы, вбиравшие в себя математику величины и направления, и сквозь теорию вероятностей, «определяемую», как подчеркивал Купер, "строго в терминах генеральных совокупностей" и иллюстрируемой стопками диаграмм Венна. Потом Купер мог предложить какой-то конкретный пример или намек и мне, по крайней мере, на мгновение, удавалось различить что-то из полезности и красоты математики.

Как-то после обеда Купер сказал нам, чтобы каждый написал свой день рождения на листке бумаги, сложил его вдвое и передал вперед. Он поднял над головой пятидолларовую банкноту. "Держу пари, что как минимум у двоих из вас один и тот же день рождения. Желающие есть?"

— Ставлю свои пять, — сказал один из волейболистов. Еще семь-восемь человек выложили по пять долларов на свои столы. Поразмыслив, я решил, что раз в году 365 дней, но в классе только порядка 50 студентов, Купер давал нам шанс выиграть легкие деньги. Однако, убедившись за последние несколько дней, что все мои ответы оказывались неверными, свои доллары я оставил нетронутыми в заднем кармане. Купер развернул первый лист и вслух прочел дату. Поднялись три руки. Студенты, выложившие деньги, застонали, в то время как все прочие кругом смеялись.

Углубив нас в математику, Купер продемонстрировал, что в группе нашего размера вероятность совпадения двух дней рождений превышает 90 процентов. [2]Затем он отложил кусочек мела и прошелся по комнате, собирая урожай пятидолларовых банкнот. "Один из уроков, которые мы хотим вам здесь преподать, — жизнерадостно сообщил он, — это тот факт, что строгие математические рассуждения могут принести большую выгоду".

По окончании каждого послеполуденного занятия я совершал небольшие пробежки по кэмпусу, чтобы рассеяться. Потом покупал себе в буфете кусок пиццы с банкой диетической пепси и шел обратно в Вилбур-холл, общежитие для студентов, к которому я был приписан вплоть до начала основного курса.

В моей комнате имелись две металлические кровати, по типу армейских, с замызганными матрасами, еще пара больших, помятых металлических столов и два обшарпанных деревянных шкафа. Здесь я пригибал гусиную шею заржавленной лампы ближе к своим книгам и начинал решать задачи.

Задачи, например, вот такого типа:

Если связь между совокупными затратами и числом изготовленных единиц продукции линейная, и если затраты увеличиваются на $5 при изготовлении каждой единицы продукции, и если совокупные затраты на выпуск 100 единиц продукции составляют $600, то каким уравнением будет описываться связь между совокупными затратами и количеством изготовленных единиц продукции?

Или, скажем, мне встречалась такая задача:

Какие значения x удовлетворяют следующему уравнению?

x 2— 8 x + 15 = 0

Или вот еще такая:

Пусть многочлен

y = p( x ) = a n x n+ a n-1 x n-1+… + a 1 x + a 0

представляет собой полиномиальную функцию. Пользуясь теоремами, которые мы обсуждали в классе, решить следующее уравнение:

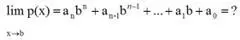
[3]

Когда по истечении двух-трех часов уже не оставалось сил все это выносить, я спускался в холл к телефону-автомату, вытаскивал кредитную карточку и звонил своей подруге, Эдите, в Феникс.

Эдита работала через коридор от меня в Белом доме, в службе деловых переговоров. Мы встречались уже года два, но так как никто из нас не ощущал себя готовым к браку, было решено проверить чувства испытанием, расставшись на некоторое время. Пока я был в Стенфорде, Эдита пробовала свои силы в аспирантуре международного менеджмента при Американском университете. Она поменяла Вашингтон на Аризону недели за две до моего отъезда в Калифорнию.

— Меня здесь тошнит, — говорила Эдита.

— Тебя там тошнит? — отвечал я. — Меня тут тошнит.

— Подними мне настроение.

— Нет, это ты мне подними настроение.

— Нет, ты первый.

Эти звонки стали ранним, еще не вполне осознаваемым предвестником феномена, который в конечном итоге нам обоим пришлось признать. Бизнес-школа — враг романтики.

Потом я звонил родителям.

— Мне это напоминает твои первые недели в оксфордской аспирантуре, — говорила мне мать. — Разве ты не помнишь, с каким трудом привыкал к Англии?

— Тут дела по-другому, — отвечал я. — У меня уже годы не те. Тебе не кажется странным, что зрелый мужчина в тридцать один год звонит родителям в поисках утешения?

— Боже сохрани, конечно, нет! Родители всегда останутся родителями. Ты просто держись.

Затем трубку брал отец.

— Пап, ты сам чего думаешь? Может, мне взять и вернуться обратно в Вашингтон, поискать там чего-нибудь в пиаре, а?

— Ты все обдумал сам, прежде чем ехать, — отвечал отец. — Сейчас ты обязан перед самим собой продержаться, по крайней мере, до Рождества.

Затем я звонил Конору.

— Ну, как учеба? — интересовался я.

— Учеба-то? — отвечал Конор. — Нашего маленького вот уже с полчаса как рвет. Желудочный грипп. Если мне удастся уложить его спать, то смогу приступить к куперовским задачкам. Но я и так знаю, что ничего в них не пойму и к тому времени уже сам буду полусонный.

И пусть разговоры с подружкой и родителями давали мало утешения, такого рода беседы с Конором всегда несколько поднимали мой дух. Конор страдал от тех же напастей, что я сам, и к тому же ему было еще хуже.

Обычно я занимался по ночам до часу или двух утра, желтым фломастером делая пометки в учебниках, а потом принимался за задачи. Хотя чтение и перечитывание текстов шло со скрипом, на второй или третий день я начинал уже понимать приличную порцию материала. И даже когда мои ответы оказывались неверными, — что было сплошь и рядом, — порой удавалось уловить, где именно я ошибся. ("Может, в конце концов, я справлюсь-таки с этой математикой", — начинал подумывать я.)