Энн Ветемаа - Вся правда о русалках. Полевой определитель

— Мочь и силу?

— Я не знаю, как еще сказать… И тогда я какое-то время витаю под знаком этой силы и мочи и все натуживаюсь и натуживаюсь, чтобы стать снопом. После сильной натуги пробегает своеобычная волна, [5] «Своеобычная волна» известна в гидродинамике как солитон. Ниже мы еще к ней вернемся. словно котомка по поверхности воды, и тут я сразу становлюсь снопом. Часть силы и мочи всегда еще остается. Она продолжает витать. О ней я уже больше ничего не знаю, когда сама становлюсь снопом. При обратном превращении в русалку мы как бы снова сплавляемся вместе…

Как видно, объяснение давалось ей нелегко. Впрочем, это вполне естественно: ведь даже люди, наделенные от природы поразительным даром скоростного устного счета, не могут объяснить, как они это делают. А уж превращение в сноп или в рогалик, конечно, еще сложнее, где уж его понять простому человеку.

— А я могу взглянуть, какая ты из себя, когда в сноп оборачиваешься?

— Да ты уж не раз видел… — Русалка потупила глаза. — Как-то даже… завалился на меня спать… Когда ты первый раз бродил по берегу реки…

Я взял ее теплую и влажную, еще не высохшую после стирки руку, и мы долго сидели молча.

Заходящее солнце окрасило водную гладь в стыдливо-красные тона. Грудь русалки вздымалась. Над нами щелкал соловей.

Я благодарен скромной полоскунье-тряпичнице за те прекрасные часы, которые мы провели и которые, возможно, ждут нас впереди. До тех пор, пока бьется мое сердце. Благодарен ей также за знания, которые исподволь приобрел. Постепенно я начал осознавать, что у русалок наличествуют жизненные циклы.

Каждое превращение требует некоторой суммарной энергии (вспомним слова русалки, что это «очень утомительно»). Таким образом, со временем возникает положение, при котором русалка не осмеливается больше предпринимать метаморфозы — кто хотел бы окончить свою жизнь снопом? Тогда русалка «совсем себя лишится» (или, по модной терминологии, трансформируется в кварк-русалку) и будет витать под знаком «силы и мочи» до тех пор, пока не встретится с другой кварк-русалкой. Воссоединившись, они могут снова трансформироваться в нормальную русалку и начать новый жизненный цикл. Но кем они станут — одной из прежних, хотя и обновленных, русалок или совсем другой, — сие уже зависит от энергии обеих кварк-русалок. (Советский ученый Руссалкин показал, что таким образом могут возникать совершенно новые виды русалок.)

Теперь должно быть ясно, почему никогда и нигде не обнаруживали останков русалок.

В принципе теория превращения довольно проста. Тем более я был поражен, когда прочитал о двух первых основных законах русалкофизики. Первый из них сформулировал английский профессор Мермейд, второй — французский академик Наяд. Но как же я сам до них не додумался?!

Представляю здесь эти два закона несколько упрощенно, однако же нисколько их при этом не искажая. ПЕРВЫЙ ЗАКОН, или принцип Мермейда:

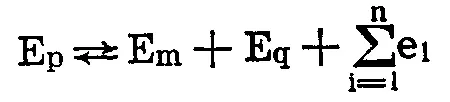
где Еp — суммарная русалкоэнергия основного образа русалки;

Em — энергетический потенциал результата превращения (сноп, известняковая плита и т. д.);

Еq — «витающий» в воздухе остаток «силы и мочи», который обычно проявляется в солитоне.

Внимательный читатель сообразит, что возможно и такое преображение:

Ер —> Em + Eg

В этом случае у русалки есть возможность какую-то часть себя оставить в качестве подарка избранному лицу. В качестве такого подарка может оказаться и золотой бокал, и известняковая плита с лошадиным навозом…

Если мы в общих чертах уясним первый основной закон, то ВТОРОЙ ЗАКОН — принцип Наяда — уже не представляет собой ничего мудреного:

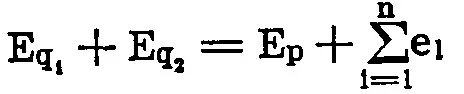
Две кварк-русалки Еq1, и Еq2 дают вместе одну нормальную русалку, чья энергия Ер плюс неизбежная потеря энергии, израсходованной на преображение, равняется сумме их первоначальных энергий.

Остается добавить, что все приведенные здесь уравнения можно было бы записать с использованием единиц массы, а не энергии, потому что они связаны между собой открытым Эйнштейном наипростейшим законом E 0 =m 0 c 2, где m 0 — масса покоя частицы, а с — скорость света в вакууме.

А теперь хотя бы чуть-чуть, совсем немножко, следует рассказать о солитоне, поскольку эта волна в последние десятилетия «привела в волнение» многие умы. Что же это за странная волна? Все мы знаем обычные волны — приятно ведь покачиваться на них в полосе прибоя. И при этом мурлыкать мужественную песню Густава Эрнесакса, в которой весьма тонко подмечено: «Поднимается волна, опускается волна». Наблюдение поэтичное и вместе с тем научно точное. Математическое уравнение описывает обычную периодическую волну с такой же прелестной поэтической образностью:

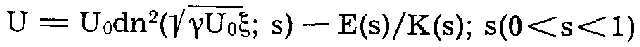
Уступая подробный разбор уравнения справочникам по гидродинамике, отметим лишь, что величина «dn» суть эллиптическая функция Якоби, a E(s) и К (s) — эллиптические интегралы. Если же теперь возникает положение S=1, то уравнение описывает солитон и принимает еще более элегантный вид:

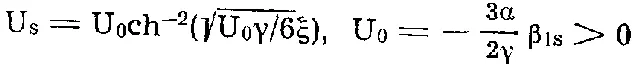
Тут-то и начинает свое движение по поверхности воды одинокая, вырвавшаяся на волю «котомка» (во всяком случае, сравнение скромной полоскуньи-тряпичницы самое образное и точное из всех до сих пор предложенных), которая, раз поднявшись из строки приснопамятной песни, более уже не останавливается и не опускается.

Солитон первым описал лорд Скотт Рассел, который в первой половине прошлого столетия, гарцуя в одно прекрасное утро по берегу маленького канала, заметил это своеобразное образование на воде. Тут же пришпорил он своего чистокровного жеребца и понесся вдоль канала вровень с волной. Своими впечатлениями он делится с нами в статье „Report on waves" (1844). Разумеется, лорду и в голову не пришло поблагодарить за редкостное зрелище русалок, однако, будучи добросовестным исследователем, он не забыл выразить признательность своему скакуну, чуть ли не возведя его в соавторы своего труда; без верного четвероногого помощника лорд и впрямь не уследил бы за волной.

Проходит полстолетия, и статья Скотта Рассела попадает в руки фламандского математика Кортевега. Он-то и предложил приведенные выше весьма привлекательные уравнения. Его труд „On the Change of Form of long Waves advancing in a rectangular Channel and on a new Type of long stationary Waves" увидел свет в 1895 году. Этот гениальный труд тоже более полустолетия находился в забвении. Ныне же уравнение Кортевега — де Врие оказалось в центре внимания физиков и метеорологов, инженеров-строителей, исследователей арочных перекрытий и многих других. Это уравнение посредством различных своих решений объясняет происходящие в горах таинственные авиакатастрофы, неожиданные разрушения куполообразных строений и даже загадочные болезненные явления в человеческом организме.