Анатолий Маклаков - Познавательные психические процессы: Хрестоматия

<���… > Выводя свой логарифмический закон, Фехнер ошибочно предполагал, что минимальный прирост ощущения ( ΔS ) будто бы есть постоянная величина на всем протяжении психологической шкалы. Хотя он хотел предположить, что постоянным является отношение едва заметного изменения раздражителя ( ΔR) 2 к его исходной величине (R), т. е.

ΔR/R = k (закон Вебера),

у него получилось, что постоянно ΔS . Из этих двух предположений он вывел отношение:

S = k log R

и тем самым нанес большой вред всему делу.

<���… > Предположим, что Фехнер принял бы положение о постоянстве отношения не только для е. з. р. стимуляции ΔR , также и для субъективного коррелята е. з. р. – ΔS . Тогда он смог бы написать:

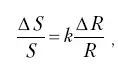
откуда следовало бы, что психическая величина S является степенной функцией физической величины R. Однако он отбросил это предположение, когда оно впервые было сделано Брентано. В результате временной победы Фехнера в психофизике открылся период бесплодных исследований, когда казалось, что нет более интересной работы, чем измерение е. з. р. Так логарифмический закон стал «пещерным идолом».

<���….> Начиная с 30-х годов XX века значение психофизики стало восстанавливаться. Новый интерес к очень старой проблеме сенсорного ответа возник благодаря изобретению методов, описывающих соотношение входа и выхода сенсорных систем. Эти методы показывают, что сенсорные ответы возрастают по степенному закону. При изучении поведения так редко удается показать, что простое отношение сохраняется при самых различных видах стимуляции, что широкое распространение и постоянство степенного закона действительно приобретают большое значение.

Конечно, можно себе представить, что ощущения всех модальностей возрастают одинаково с увеличением интенсивности стимуляции. На самом деле это совсем не так, и это легко доказать при помощи элементарного сравнения. Заметьте, что, например, происходит при удвоении освещенности пятна света и, с другой стороны, силы тока (частота 60 Гц), пропускаемого через палец. Удвоение освещенности пятна на темном фоне удивительно мало влияет на его видимую яркость. По оценке типичного наблюдателя, кажущееся увеличение составляет всего лишь 25 %. При удвоении же силы тока ощущение удара увеличивается в десять раз.

<���… > Степенная функция имеет то преимущество, что при использовании логарифмического масштаба на обеих осях она выражается прямой линией, наклон которой соответствует значению показателя. Это видно на рис. 1.4: медленное увеличение яркостного контраста и быстрое усиление ощущения удара электрическим током. Для сравнения на этом рисунке показана также функция оценки видимой длины линий, сделанной несколькими наблюдателями. Здесь, как и следовало ожидать, показатель функции лишь немного отличается от 1,0. Иначе говоря, для большинства людей отрезок 100 см кажется вдвое длиннее, чем отрезок 50 см.

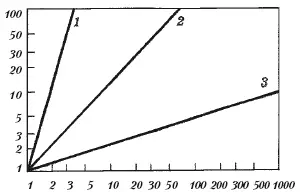
Рис 1.4.Зависимости субъективной величины (ощущения) от величины раздражителя для трех модальностей, представленные в логарифмическом масштабе на обеих осях. 1 . Электрический удар. 2. Кажущаяся длина. 3. Яркость. Абсцисса – величина раздражения (условные единицы); ордината – психологическая величина (произвольные единицы)

На рис. 1.5 те же самые три функции представлены в линейных координатах.

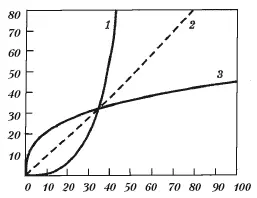
Рис. 1.5.Те же зависимости, что и на предыдущем рисунке, представленные в линейных координатах. Форма функции, вогнутая или выпуклая, зависит от величины показателя степени: n больше или меньше 1,0. Обозначения кривых и осей те же, что и на предыдущем рисунке

<���…> В своей практике автор еще ни разу не встретил исключения из этого закона (отсюда и смелость называть эту зависимость законом).

В табл. 1.1 указаны показатели степенных функций некоторых из исследованных континуумов.

Немного найдется ученых, которые бы не ощущали неудовлетворения вышеописанным методом, надежность которого всецело полагается на выражение мнения наблюдателей. И зависит от того, насколько хорошо они знают числовую систему. Эта неудовлетворенность методом вполне обоснованна, ибо поверхностные знания чисел, особенно отсутствие понятия о пропорции, естественно, затрудняют способность некоторых наблюдателей хорошо выполнить свою роль в этих экспериментах. Обозначение силы ощущения числом не является чем-то таким, что человек выполняет с большей точностью и уверенностью, хотя обыкновенный выпускник высшего учебного заведения, как правило, может производить целый ряд непротиворечивых числовых оценок.

Однако интересно не то, уверены или не уверены мы в полноценности этого метода. Интересно другое: можем ли мы подтвердить правильность степенного закона, вообще не предлагая наблюдателям производить численные оценки? Если да, можем ли мы проверить правильность отношений между показателями, приведенными в табл. 1.1? Утвердительный ответ на этот вопрос дают результаты проведения эксперимента по методу, согласно которому наблюдатель производит уравнивание интенсивностей ощущений двух различных модальностей.

Таблица 1.1

Характерные показатели степенных функций, соотносящих психологическую величину с величиной стимуляции в протетических континуумах

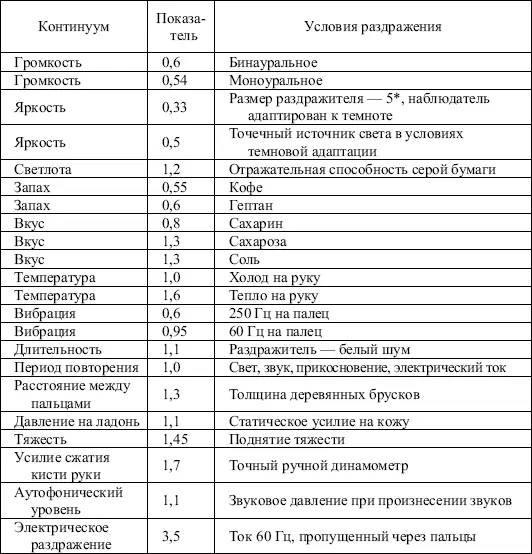
Посредством таких межмодальных сравнений, производимых при разных интенсивностях стимуляций, можно получить «функцию равных ощущений», а затем сравнить ее с такой же функцией, предсказанной на основании величин показателей для этих двух модальностей.

Если обе модальности при соответствующем выборе единиц описываются уравнениями:

S 1= R 1 m и S 2= R 2 n

и если субъективные величины S 1и S 2уравниваются путем межмодального сравнения на различных уровнях стимуляции, то результирующая функция равных ощущений примет вид:

R 1 m = R 2 n

или в логарифмах

lg R 1 = n/m Ig R

Иначе говоря, в логарифмических координатах функция равных ощущений будет прямой линией, наклон которой определяется отношением двух данных показателей.

Что касается самого эксперимента, то вопрос заключается в том, способны ли наблюдатели делать межмодальные сравнения и могут ли быть предсказаны эти сравнения, исходя из шкалы отношений кажущихся величин, определяемой независимо путем оценки величин? Способность наблюдателей высказывать простые суждения о кажущемся равенстве была установлена в другом контексте.