Анатолий Маклаков - Познавательные психические процессы: Хрестоматия

Мы можем взять рисунки с двойственным восприятием глубины. Эти рисунки (например, куб Неккера, рис. 1.17) вызывают попеременно то одно, то другое восприятие глубины и даже то один, то другой сетчаточный образ, хотя входная информация остается неизменной.

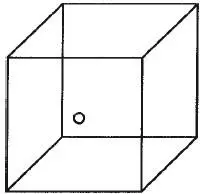
Рис. 1.17.Этот рисунок меняется по глубине: плоскость куба, отмеченная небольшим кружком, иногда кажется расположенной спереди, иногда сзади. Можно считать, что подобное чередование восприятия глубины представляет собой смену перцептивных «гипотез». Зрительная система принимает то одну, то другую гипотезу, никогда не останавливаясь ни на одном решении. Этот процесс происходит при обычном восприятии, но тогда, как правило, существует единственное однозначное решение

Теперь, если мы внимательно посмотрим на куб Неккера, то обнаружим, что хотя поверхности куба меняют свое расположение по глубине , они не изменяются по величине. Этот факт прямо говорит нам о том, что механизм константности здесь не вовлекается, не приводится в действие признаками глубины, изображенными линейным образом на бумаге. Если мы сделаем светящийся куб (проволочную модель, покрытую светящейся краской, чтобы она была видна в темноте, благодаря чему мы исключаем влияние структурного фона бумаги на восприятие), то получим совершенно иные результаты. Когда наш светящийся куб изменяется по глубине, он сразу же изменяется и по форме. Та поверхность куба, которая воспринимается как дальняя, кажется больше, хотя обе поверхности куба фактически одинаковой величины. Таким образом, мы видим на этом примере, что закон Эммерта применим и к двойственным изображениям. Если мы сделаем настоящий трехмерный куб, то обнаружим, что, когда он переворачивается в нашем восприятии, мы видим вместо куба усеченную пирамиду, поскольку та поверхность куба, которая кажется ближе, выглядит меньше, чем та, которая воспринимается как более удаленная; здесь константность действует в обратном порядке, в соответствии с видимой, а не истинной глубиной, что и приводит к искажениям величины при изменении восприятия глубины. Этот факт может убедить в том, что восприятие глубины, по существу, связано с константностью; однако рассмотрим следующие факты. Возьмем рисунок куба, изображенный на бумаге, но с добавочной линией, как показано рис. 1.18. Эта линия, несмотря на то что она фактически прямая, кажется изогнутой в том месте, где она пересекает угол куба. Теперь тщательно проследите за этой линией, когда куб изменяется (неожиданно) по параметру глубины. Вы увидите, что линия продолжает казаться изогнутой точно таким же образом. Здесь мы видим нечто совершенно иное по сравнению с тем, что происходит, когда подобная линия добавляется к настоящему трехмерному светящемуся кубу: тогда линия будет тоже казаться изогнутой (вследствие константности), но направление изгиба меняется, когда восприятие куба изменяется по глубине.

Изгиб линии, пересекающий угол нарисованного куба, определяется не тем, кажется ли этот угол внутренним или внешним, а просто тем, является ли этот угол внутренним или внешним в обычных условиях трехмерного восприятия.

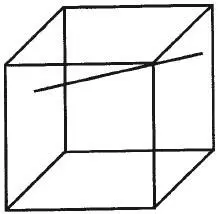
Рис. 1.18.Линия, пересекающая угол куба Неккера, кажется слегка изогнутой, хотя фактически она прямая. Она кажется такой же изогнутой и тогда, когда куб переворачивается по глубине. Из этого следует, что иллюзионный изгиб линии не является результатом воспринимаемой глубины. Но если сделать светящуюся модель куба, направление изгиба линии будет меняться с каждым изменением ориентации куба

Это важное обстоятельство, так как оно подтверждает, что иллюзорное искажение линии возникает не вследствие механизма константности, действующего в соответствии с видимой глубиной, а прямо согласуется с признаками глубины, хотя бы им и противоречила фактура бумаги, из-за которой куб кажется плоским. Если мы поместим линию, подобную этой, поперек светящегося куба, то направление изгиба этой линии будет изменяться с изменением ориентации куба в нашем восприятии; здесь закон Эммерта перестает действовать.

Можно измерить видимую глубину, восприятие которой возникает благодаря перспективе или другим признакам глубины; это можно сделать с помощью ряда технических приемов, обеспечивающих объективное измерение видимой глубины. С помощью этих приемов (предложенных автором) можно прямо соотнести видимую глубину с иллюзиями.

Довольно легко вычислить меру иллюзии типа искажений величины или формы, о которых идет речь в этой главе. Это можно сделать с помощью набора различных линий или форм, предложенных наблюдателю, с тем чтобы он выбрал среди них ту, которая больше всего похожа на рисунок, вызывающий иллюзию, как видит ее сам наблюдатель. Разумеется, важно показывать наблюдателю сравниваемую с образцом линию так, чтобы она не искажалась! В опыте иногда лучше использовать такое приспособление, которое дает возможность наблюдателю или экспериментатору производить непрерывное подравнивание сравниваемой линии или набора линий с образцом. Такое приспособление для сравнения линий показано на рис. 1.19.

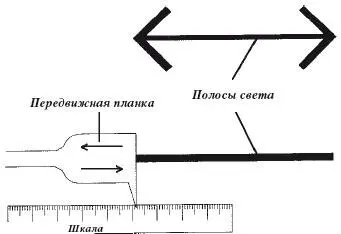
Рис. 1.19.Как измерить иллюзию. Наблюдатель смотрит на стрелу и сравниваемую с ней линию, которую он устанавливает так, чтобы она оказалась той же длины, что и искаженная стрела. Таким образом можно непосредственно измерять степень иллюзии. (Измерение, однако, возможно только тогда, когда иллюзия не является логически парадоксальной.) На рисунке показано, как выглядит аппаратура сзади, со стороны экспериментатора

Труднее измерить видимую глубину. Это может показаться даже невозможным. Но рассмотрим рис. 1.20. Рисунок освещается сзади, чтобы избежать влияния фактуры фона на восприятие, и виден через экран поляроида. Другой экран поляроида помещается над одним глазом под углом к первому так, чтобы свет от рисунка не достигал этого глаза. Между глазами и рисунком помещается стекло, покрытое с одной стороны тонким слоем амальгамы, через которое виден рисунок и которое также отражает одно или несколько небольших источников света, вмонтированных в оптическую линейку. Эти источники света кажутся расположенными на рисунке. Конечно, с точки зрения оптических законов, они действительно находятся на рисунке, но только в том случае, когда расстояние от источников света до глаз равно расстоянию от рисунка до глаз. Однако маленький источник виден обоими глазами, в то время как рисунок виден только одним глазом, потому что другой закрыт поляроидом. Передвигая источники света по оптической линейке, мы можем поместить их таким образом, что они будут казаться расположенными на том же самом расстоянии от наблюдателя, что и любая часть рисунка. Если рисунок имеет перспективу или другие признаки глубины, тогда наблюдатель помещает источники света не на истинном расстоянии, которое отделяет его от рисунка, а на том, которое, как ему кажется, отделяет его от той части рисунка, на которую он наводит световое пятно. Для людей с нормальным бинокулярным восприятием глубины это довольно простая задача, и таким способом можно измерить кажущуюся глубину.