Анатолий Маклаков - Познавательные психические процессы: Хрестоматия

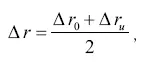
вычисление которой оправданно в случае, когда Δ r 0и Δ r и близки друг к другу.

Третий главный психофизический метод, как было сказано выше, – это метод постоянных раздражений, или метод истинных и ложных случаев. При пользовании этим методом определение искомых величин абсолютного или разностного порога производится уже не столь прямым образом, как посредством двух вышеописанных методов, но лишь на основании статистической обработки достаточно большого числа показаний испытуемого. Метод состоит в следующем. Раздражители различной интенсивности предъявляются испытуемому в беспорядочной последовательности. Если дело идет об определении разностного порога, раздражители эти предъявляются, чередуясь с нормальным. От испытуемого требуется при этом оценить, кажется ли ему переменный раздражитель больше нормального или меньше его или же кажется равным раздражителю нормальному. В случае определения абсолютного порога испытуемый просто должен говорить, ощущает он или не ощущает предъявляемое ему раздражение. Сама величина порога вычисляется в результате подсчета правильных и ложных ответов, данных испытуемым при многократной оценке предъявлявшихся ему в беспорядке раздражителей разной интенсивности. Значение этих раздражителей или же разность (D) между ними и каким-либо раздражителем, являющимся нормальным, через небольшие равные ступени откладываются по абсциссе; по ординате откладываются частоты ответов, данных испытуемым, – ответов правильных, ложных и неопределенных.

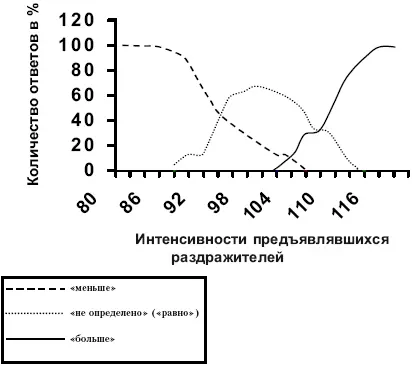
Рис. 1.1.Графическое изображение результатов измерения разностных порогов постоянных раздражений. В качестве нормального служило раздражение, равное 100

На рис. 1.1 показана в качестве примера запись результатов измерения разностных порогов по методу постоянных раздражителей. При этом берут не абсолютное количество таких ответов, полученных для различных раздражителей, а их относительное количество по отношению к общему числу всех оценок данного раздражителя. Оценки неопределенные (т. е. такие, в которых испытуемый затрудняется сказать, больше или меньше нормального данный раздражитель) Фехнером причислялись поровну к оценкам правильным и к оценкам ложным. Пороговому значению S в таком случае соответствует такое значение D, на которое падает одинаковое количество оценок правильных и ложных, т. е. значение D, оценивающееся правильно в 50 % всех предъявлений. Допуская, что наши оценки, даваемые раздражителям в зависти от величины этих последних, подчиняются закону Гаусса, Фехнер приходит к выводу, что относительное количество правильных ответов «больше» r/n (где r есть число правильных ответов, а n – общее количество ответов) зависит от величины D (т. е. разности данного раздражителя с нормальным) следующим образом:

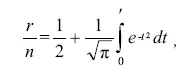
а относительное количество ложных ответов, «меньшее» — ∫/n, соответственно выражается уравнением:

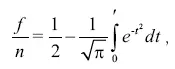
в этих формулах t = h-D, где h — мера точности, а e – основание логарифмов Непера. Фехнером даются специальные, так называемые фундаментальные таблицы к методу истинных и ложных случаев. В этих таблицах для разных значений r/n вычислены соответствующие им значения t, что позволяет, зная r/n и D, находить h. Последнюю же величину Фехнер и рассматривает как искомую меру чувствительности.

Г. Э. Мюллер в отличие от Фехнера считает необходимым посредством метода истинных и ложных случаев определить не только меру точности h, но и самую величину разностного порога S 3.

Для вычисления ее были предложены различные способы. Мы укажем здесь на следующие формулы. При определении верхнего разностного порога, т. е. разностного порога в сторону более сильного раздражителя,

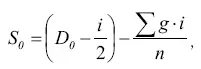
где S 0 – величина раздражителя, соответствующая верхнему разностному порогу;

D 0 – максимальная величина раздражителя (при этой интенсивности все ответы испытуемого должны быть правильными);

i — величина постоянного интервала между интенсивностями предъявляемых в беспорядке переменных раздражителей;

Σg – сумма всех ответов «больше» («сильнее»);

n — общее число всех ответов, получаемых от испытуемого для каждой отдельной величины переменного раздражителя (число это для каждого из переменных раздражителей должно быть одинаковым).

При определении нижнего разностного порога (т. е. разностного порога в сторону более слабого раздражителя)

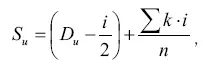
где S u– величина раздражителя, соответствующая этому порогу;

D u– минимальная величина интенсивности применявшегося переменного раздражителя, при которой все ответы испытуемого должны быть правильными;

Σk – сумма всех ответов «меньше» («слабее»),

Разность между величинами S 0и S uбудет характеризовать ту область переменных раздражителей, которая вызывает у испытуемого оценки «равны» («одинаковы»):

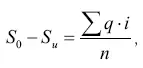
где Σg — сумма всех ответов «равны». Верхний разностный порог будет, очевидно, равен S 0 – N, где N — величина нормального раздражителя, а нижний разностный порог будет равняться соответственно S и– N.

Вышеприведенные формулы вытекают из рассмотрения идеальных прямоугольников, к которым могут быть приведены площади, очерчиваемые кривыми частоты ответов «меньше», «равны» и «больше», даваемыми в эксперименте, проведенном по методу постоянных раздражений.

Для вычисления посредством этих формул не разностного, а абсолютного порога надо лишь собрать и подсчитать ответы «нет», «неопределенно» и «есть» (вместо ответов «меньше», «равны» и «больше») (Pauli, 1923).

Упрощенную интерполяционную формулу для вычисления порогов по методу постоянных раздражений находим у Вундта (Wundt, 1908). Именно пороговое значение D = D u , по Вундту, соответствует тому значению раздражителя, которое в 50 % всех случаев оценивается правильно.