Дмитрий Ушаков - Психология интеллекта и одаренности

Модель имеет сеть, включающую четыре слоя нейроноподобных элементов, или узлов. Один слой узлов является входным, два – промежуточными (или ассоциативными), четвертый – выходным. Возбуждение распространяется от первых слоев к следующим через дуги между узлами. Связи между первым и вторым, а также третьим и четвертым слоями рассматриваемой модели являются жестко фиксированными. Связи между вторым и третьим слоями могут изменяться в процессе обучения. Изменению в ходе обучения подвержен также порог активации элементов третьего слоя.

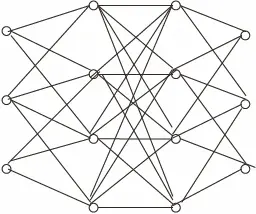
Рис. 2.13.Фрагмент сети модели Д Румелхарта и Дж. Мак-Клелланда

Если подавать на входные узлы сети активацию, сеть будет реагировать – выдавать определенный паттерн активации на выходе. Например, сеть Румельхарта и Мак-Клелланда на входе получает инфинитив глагола, а на выходе выдает прошедшее время (каждый входной и выходной узел модели кодирует один звук). Сеть можно обучать: если она выдает неправильный ответ, по определенному алгоритму модифицируются связи между ассоциативными слоями.

Наиболее интересным в моделях такого типа является то, что они показывают весьма любопытное сходство с реальным поведением людей. В частности, модель Румельхарта и Мак-Клелланда на определенном этапе обучения, как и дети, демонстрирует сверхгенерализацию (например, выдает gived вместо gave), на другом этапе – появление частных правил и т. д.

Показана способность параллельных распределенных сетей и к более сложной переработке информации. Так, Г. Хинтон создал модель, которая обучается определению родственных отношений (Hinton, 1986). На ее входные узлы подают имена людей и учат устанавливать между ними родственные отношения. Была показана способность этой модели к простым умозаключениям. Так, если дать ей некоторое количество отношений типа «Иван отец Петра», «Петр отец Сидора», «Иван дед Сидора», то сеть из «Джон отец Джека» и «Джек отец Джима» может сама вывести «Джон дед Джима». Интересно, что анализ функционирования отдельных узлов промежуточных слоев показывает образование понятий, таких как пол, поколение, принадлежность к семье и т. д. Другими словами, некоторые узлы срабатывали только в отношении лиц старшего поколения, другие – только в отношении женщин и т. д.

Коннекционистские модели обладают определенной привлекательностью в силу ряда причин: подобия нашей нейрофизиологической организации (или по крайней мере тому, что мы о ней сегодня знаем), способности естественным образом моделировать некоторые процессы, высокой точности и возможности компьютерного моделирования, но при принципиальном отличии по архитектуре от компьютера и т. д. Они позволяют объяснить такие феномены, которые оказываются непонятными для информационных моделей, лишенных сетевой составляющей. К таким феноменам относится, например, облегчающее влияние контекста на решение задач.

В то же время некоторые авторы высказывают сомнение по поводу того, что коннекционизм может стать главным средством моделирования познавательных процессов. Так, Дж. Фодор и З. Пылишин доказывают, что коннекционистские модели в принципе не обладают вычислительной мощью, позволяющей выполнять в полном объеме пропозициональное исчисление, и, следовательно, не могут объяснить всех возможностей познавательной системы человека.

Специально рассмотрим вид сетей, предложенный Дж. Хопфилдом, поскольку эти сети привлекли особое внимание в контексте проблемы творчества. В этих сетях каждый нейрон может принимать одно из двух состояний. В них нет входных, промежуточных и выходных слоев, однако, как показано на рисунке 2.14, есть обратные связи.

За счет обратных связей сети Хопфилда являются динамическими, т. е. выход, передаваясь по сети обратной связи, модифицирует вход. Затем новый вход модифицирует выход, и процесс повторяется снова и снова. Для устойчивой сети последовательные итерации приводят к все меньшим изменениям выхода, пока в конце концов выход не становится постоянным. Для некоторых сетей процесс никогда не заканчивается, такие сети называют неустойчивыми.

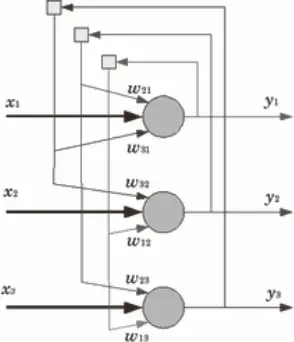
Рис. 2.14.Сеть Хопфилда

Во время работы сети Хопфилда признаком нахождения решения является момент, когда достигается аттрактор, статический (когда на каждом следующем шаге повторяется устойчивое состояние) или, возможно, динамический (когда до бесконечности чередуются два разных состояния). Это конечное состояние сети и является ее реакцией на данный образ.

На первом этапе сеть Хопфилда обучают. Это означает, что сеть запоминает определенное количество состояний.

Матрица весовых коэффициентов настраивается детерминированным алгоритмом раз и навсегда, и затем весовые коэффициенты больше не изменяются.

Как только веса заданы, сеть может быть использована для получения запомненного выходного вектора по данному входному вектору, который может быть частично неправильным или неполным.

Обычно ответом является такое устойчивое состояние, которое совпадает с одним из запомненных при обучении векторов, однако при некоторых условиях (в частности, при слишком большом количестве запомненных образов) результатом работы может стать так называемый ложный аттрактор («химера»), состоящий из нескольких частей разных запомненных образов, а также в синхронном режиме сеть может прийти к динамическому аттрактору.

Если во время обучения сформировать матрицу весовых коэффициентов (межнейронных связей) на основании эталонных образов, то нейронная сеть в процессе работы будет менять состояния нейронов до тех пор, пока не перейдет к одному из устойчивых состояний.

Внешнее воздействие на хопфилдовскую сеть заключается в том, что некоторые ее узлы приводятся в состояние активации. Затем сеть, предварительно обученная на распознавание определенных образов, начинает самопроизвольно эволюционировать, пока не доходит до устойчивого состояния, в котором и остается. Состояние, в которое она приходит, означает, что образ распознан. Сеть Хопфилда отличается способностью переходить от разных исходных состояний к одному и тому же конечному, т. е. несколько различные образы она может распознать как один и тот же объект. Эти конечные устойчивые состояния сети, или, пользуясь синергетической терминологией, аттракторы задаются предварительным обучением.

Представим сеть Хопфилда, распознающую зрительные образы, каждый элемент которой соответствует определенной точке сетчатки. Допустим, сеть обучена распознавать какой-то известный портрет Пиаже, т. е. возбуждение участков сетчатки при восприятии этого портрета является аттрактором системы. Если мы дадим теперь на вход сети несколько иное изображение ученого, то после большего или меньшего количества итераций система придет к состоянию, соответствующему тому портрету, на который было проведено научение, т. е. «узнает» Пиаже.