Маркус дю Сотой - Искусство мыслить рационально. Шорткаты в математике и в жизни

1, 2, 4, 8, 16 …

Что, если я скажу вам, что следующее число в этой последовательности – не 32, а 31?

Если взять круг, отмечать на его окружности точки и соединять все эти точки прямыми линиями, каково будет максимальное число областей, на которые можно разделить этот круг? Если точка всего одна, никаких линий не будет и область получится тоже всего одна. Если добавить еще одну точку, две точки можно соединить линией, которая разделит круг на две области. Добавим третью точку. Проведя все возможные линии, соединяющие эти точки, получим треугольную фигуру, окруженную тремя секторами круга: всего четыре области.

Рис. 1.1. Первые пять чисел деления круга

Если продолжить действовать таким же образом, кажется, что проявляется паттерн. Вот данные по числу областей, получающихся при добавлении очередных точек на окружности:

1, 2, 4, 8, 16 …

В этот момент разумно предположить, что добавление очередной точки удваивает число областей. Проблема заключается в том, что этот паттерн нарушается, как только я добавляю шестую точку. Как ни старайся, число областей, на которые линии разбивают круг, оказывается равным 31. А вовсе не 32!

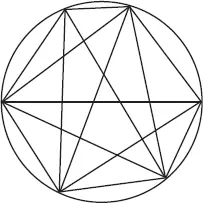
Рис. 1.2. Шестое число деления круга

Для числа областей существует формула, но она чуть сложнее, чем простое удвоение. Если на окружности есть N точек, максимальное число областей, которые можно получить, соединяя эти точки, равно

1/24 ( N 4– 6 N 3+ 23 N 2– 18 N + 24).

Мораль тут следующая: важно знать, что именно описывают ваши данные, а не полагаться на одни лишь числа. Обработка данных может быть делом опасным, если она не сочетается с глубоким пониманием того, откуда взялись эти данные.

Вот еще одно предостережение относительно шорткатов такого рода. Каким должно быть следующее число в этой последовательности?

2, 8, 16, 24, 32 …

В ней много степеней двух. Но что там делает число 24? В общем, если вы сумели заключить, что следующее число этой последовательности – 47, я советую вам в ближайшую же субботу купить лотерейный билет. Это выигрышные номера тиража британской Национальной лотереи, разыгранного 26 сентября 2007 года. Мы настолько пристрастились к поиску паттернов, что часто видим их там, где никакого паттерна ожидать нельзя. Лотерейные билеты выпадают случайным образом. Без паттернов. Без тайных формул. Шорткатов к миллионным состояниям не бывает. Однако в главе 8 я объясню, что даже случайные вещи следуют неким паттернам, которые можно рассматривать в качестве потенциальных шорткатов. Если речь идет о случайностях, шорткатом будет рассмотрение долгосрочной перспективы.

Концепцию паттерна можно использовать в качестве шортката к пониманию того, действительно ли какое-либо явление случайно, и этот метод имеет отношение к легкости запоминания числовых последовательностей.

Поскольку в интернете каждую секунду появляется огромное количество данных, компании ищут более рациональные способы их хранения. Выявление паттернов в данных облегчает их сжатие, благодаря которому для их хранения требуется меньше места. Именно эта идея лежит в основе технологий, подобных форматам JPEG или MP3.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Английское слово shortcut , центральное в этой книге, не имеет точного аналога в русском языке. Его часто переводят выражением «короткий путь», но оно не вполне передает нужное значение. Такой путь далеко не всегда бывает физически более коротким: он может быть более быстрым, более легким, более удобным и т. д. Поэтому кажется целесообразным использовать в переводе этой книги слово «шорткат», уже существующее (особенно в контексте информатики), хотя еще и не вполне закрепившееся, в русском языке. – Здесь и далее, если не указано иное, примеч. перев .

Историческая достоверность этого эпизода небесспорна: в точности то же самое рассказывают, например, о Лобачевском и о Спинозе. Это, однако, нисколько не умаляет ни гениальности всех этих мыслителей, ни изящества решения.

При заданном объеме.

Еще одно богатое значениями английское слово, которое, кажется, лучше позаимствовать, чем передавать многословными выражениями. В зависимости от контекста оно может означать рисунок, узор, канву, выкройку, шаблон, систему, характер, закономерность и т. д. Трудность перевода слова pattern на другие языки обсуждается и в главе 3 этой книги.

Дифференциальное и интегральное исчисление.

Этот разговор происходит в начале 4-й главы 1-й книги трилогии.

The Simpsons, S06E04, Itchy & Scratchy Land (1994).

Из эссе «Критик как художник» (The Critic as Artist, 1891), пер. с англ. А. М. Зверева. Цит. по: Уайльд О. Собр. соч.: В 3 т. М.: Терра – Книжный клуб, 2003. Т. 3.

Из первого эссе серии «Бездельник» (The Idler), публиковавшейся в лондонском еженедельнике Universal Chronicle с апреля 1758 по апрель 1760 г.

Цит. по: Кристи А. Автобиография / Пер. с англ. В. Чемберджи, И. Дорониной. М.: Вагриус, 1999.

Хоум-ран ( home run ) – игровая ситуация, в которой отбивающий игрок успевает обежать все четыре «базы» поля, пока отбитый им мяч не окажется в руках игрока команды противника. Если ему удается отбить мяч за пределы поля, хоум-ран засчитывается автоматически.

Легко заметить, что эти слова родственны русским «практика» и «поэзия». В классификации Аристотеля был и третий вид деятельности – теория (θεωρία), то есть деятельность, направленная на познание истины.

Цит. по: Маркс К. Критика Готской программы // Избранные произведения: В 2 т. / Под ред. М. Б. Митина. М.: ОГИЗ, Государственное издательство политической литературы, 1940. Т. II. С. 453.

Цит. по: Маркс К. Капитал. Критика политической экономии. / Пер. с нем. И. И. Степанова-Скворцова, испр. и доп. Т. 3. Ч. 1 и 2. М.: Государственное издательство политической литературы, 1951. С. 833.