БСЭ - Большая Советская энциклопедия (ГЕ)

Лит.: Иванченко А. А., Трудовые ресурсы экономических районов СССР и проблемы рационального их использования, в сборнике: Вопросы размещения производства в СССР, М., 1965; Дегтярь Л. С., Трудовые ресурсы и их использование в зарубежных социалистических странах — членах СЭВ, М., 1969.

С. А. Ковалев.

Геогра'фия физи'ческая, см. Физическая география.

Геогра'фия экономи'ческая, см. Экономическая география .

Геодези'ческая астроно'мия, раздел практической астрономии , наиболее тесно связанный с геодезией и картографией; изучает теорию и методы определения широты j и долготы l места, а также азимута а направления на земной предмет и местного звёздного времени s из астрономических наблюдений при геодезических и картографических работах. Т. к. эти наблюдения производятся в полевых условиях, то Г. а. часто называют полевой астрономией. Точка земной поверхности, в которой широта, долгота и азимут определены из астрономических наблюдений, называется астрономическим пунктом . Предмет Г. а. состоит в изучении: а) переносных астрономических инструментов, б) теорий наблюдения небесных светил и методов определения j , l , а и s и в) методов обработки результатов астрономических наблюдений. В Г. а. применяются малые, или переносные, астрономические инструменты, позволяющие измерять зенитные расстояния и направления на небесные светила, а также горизонтальные углы между различными направлениями. Основными инструментами в Г. а. служат: универсальный инструмент , полевой хронометр и радиоприёмник для приёма сигналов времени.

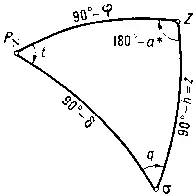
В Г. а. разработан ряд способов астрономических наблюдений, различающихся в зависимости от того, какие величины определяются (время, широта, долгота или азимут), какие светила для этого наблюдаются (звёзды или Солнце) и как и какие величины непосредственно измеряются при наблюдениях небесного светила (зенитное расстояние z , высота h , азимут а* и момент Т прохождения светила через избранную плоскость). Выбор этих способов зависит от поставленной задачи, точности её решения, наличия инструментов и т. д. При этом небесные координаты наблюдаемого светила, а именно его прямое восхождение а и склонение a , считаются известными; они приводятся в астрономических ежегодниках и каталогах звёзд.

Соединив на небесной сфере ( рис. ) полюс P N , зенит места Z и наблюдаемое светило а дугами больших кругов, получим т. н. параллактический треугольник P NZs , в котором угол при вершине Z есть дополнение азимута а* светила до 180° и угол при вершине P N равен часовому углу t светила.

Все способы астрономических определений основаны на решении параллактического треугольника после измерения его некоторых элементов (см. Сферическая астрономия ). Так, измерив зенитное расстояние Z светила в момент Т по хронометру и зная широту j места, можно определить часовой угол t светила из выражения

cosz = sinj sin d + cosj cosd cost

и по равенству t = s — a= Т + u — a найти поправку u к показанию хронометра и местное звёздное время s . Зная поправку хронометра u и измерив зенитное расстояние Z светила, можно определить широту j места. Поправку хронометра выгодно определять из наблюдений звёзд в первом вертикале , а широту места — в меридиане, т. е. в кульминации небесного светила. Если измерить зенитные расстояния двух звёзд, расположенных в меридиане к Ю. или С. от зенита места, то тогда

j = d S— z S= d N— z N.

Особенно удобны способы, основанные на измерении окулярным микрометром малых разностей зенитных расстояний северных и южных звёзд в меридиане (см. Талькотта способ ). В способах соответственных высот отмечают моменты T 1 и T 2 прохождений двух звёзд через один и тот же альмукантарат . Если известна j , то получают u (см. Цингера способ ), а если известна u , то определяют j (см. Певцова способ ). Из наблюдений серии равномерно распределённых по азимуту звёзд на постоянной высоте 45° или 30° определяют j и l (см. Мазаева способ ).

Азимут а* небесного светила определяют, измеряя его часовой угол или зенитное расстояние и зная широту j места наблюдения. Прибавляя к азимуту наблюдаемого светила (обычно Полярной звезды) горизонтальный угол Q между ним и земным предметом, получают азимут а земного предмета.

Разность долгот двух пунктов равна разности местных звёздных времён в этих пунктах или разности поправок хронометра, отнесённых к одному физическому моменту по известному ходу часов , так что l 2— l 1= s 2— s 1= (T + u 2) — (Т + u 1) = u 2— u 1+ T 2— T 1 . Долготы l отсчитываются от меридиана Гринвича. Поэтому l = s — S = u — U . Поправки хронометра u относительно местного звёздного времени s определяют из наблюдений звёзд, а U относительно гринвичского звёздного времени S — из приёма ритмических сигналов времени по радиотелеграфу. В современных высокоточных работах ошибки определения широты, долготы и азимута не превышают ± 0,5".

Лит.: Цингер Н. Я., Курс практической астрономии, М., 1924: Вентцель М. К., Полевая астрономия, ч. 1—2, М., 1938—40; Блажко С. Н. . Курс практической астрономии, М. — Л., 1951; Цветков К. А., Практическая астрономия, 2 изд., М., 1951; Кузнецов А. Н., Геодезическая астрономия, М., 1966.

А .В. Буткевич.

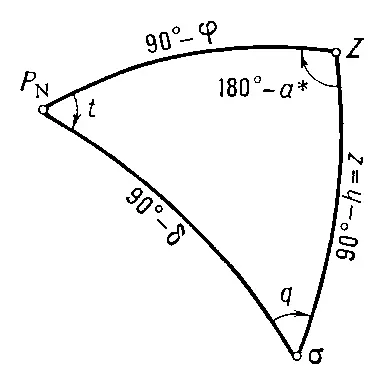
Рис. к ст. Геодезическая астрономия.

Геодезическая гравиметрия, раздел геодезии, в котором рассматриваются теории и методы использования результатов измерения силы тяжести для решения научных и практических задач геодезии. Основное содержание Г. г. составляют теории и методы определения внешнего поля потенциала W силы тяжести g Земли по измерениям на земной поверхности S и астрономо-геодезическим материалам. Г. г. включает также теорию нивелирных высот и обработку астрономо-геодезических сетей в связи с особенностями гравитационного поля Земли. Обычно из этого поля выделяют правильное и известное поле потенциала U т. н. нормальной Земли сравнения, представляемой в виде уровенного эллипсоида. Центры масс и оси вращения реальной и нормальной Земли совпадают. Основную задачу Г. г. сводят к выводу возмущающего потенциала Т = W — U , который определяют из решения граничных задач математической физики. На земной поверхности Т удовлетворяет граничному условию