БСЭ БСЭ - Большая Советская Энциклопедия (АН)

Теория А. ф. создана в 19 в., в первую очередь благодаря работам О. Коши, Б. Римана и К. Вейерштрасса. Решающую роль в построении этой теории сыграл «выход в комплексную область» — переход от действительного переменного х к комплексному переменному z = х + iy, которое может меняться в произвольной области комплексной плоскости. Теория А. ф. возникла как теория функций комплексного переменного; в некотором смысле именно аналитические (а не произвольные комплексные функции двух действительных переменных х и y ) естественно считать функциями комплексного переменного z. Теория А. ф. составляет основное содержание общей теории функций комплексного переменного. Поэтому часто под теорией функций комплексного переменного понимают именно теорию А. ф.

Существуют различные подходы к понятию аналитичности. В основе одного из них, впервые развитого Коши и далеко продвинутого Риманом, лежит структурное свойство функции — существование производной по комплексному переменному, или комплексная дифференцируемость. Этот подход тесно связан с геометрическими соображениям и. Другой подход, систематически развивавшийся Вейерштрассом, основывается на возможности представления функций степенными рядами; он связан, тем самым, с аналитическим аппаратом, которым может быть изображена функция. Основной факт теории А. ф. заключается в тождественности соответствующих классов функций, рассматриваемых в произвольной области комплексной плоскости.

Приведём точные определения. Всюду в дальнейшем через z обозначается комплексное число х + iy, где x и y — действительные числа. Геометрически число z изображается точкой плоскости с координатами х и y; евклидова плоскость, точки которой отождествляются с комплексными числами, называется комплексной плоскостью. Пусть D — область (открытое связное множество) в комплексной плоскости. Если каждой точке z области D приведено в соответствие некоторое комплексное число w, то говорят, что в области D определена (однозначная) функция f комплексного переменного z, и пишут: w = f ( z ) , z ( D. Функция w = f ( z ) = f ( x + iy ) комплексного переменного z ( D может рассматриваться как комплексная функция двух действительных переменных х и y, определённая в области D. Полагая w = u + iv, где u и v — действительные числа, замечают, что задание такой функции f эквивалентно заданию двух действительных функций j и y двух действительных переменных х и y, определённых в той же области:

u = j( x, y ) , v = y( x, y ) , ( x, y )Î D.

Пусть z — фиксированная точка области D . Придадим z произвольное приращение D z = D x + i D y (так, чтобы точка z +D z оставалась в пределах области D ) и рассмотрим соответствующее приращение функции f : D f ( z ) = f ( z + ( z ) — f ( z ) . Если разностное отношение D f ( z )/D z имеет предел при Dz®0, т. е. существует комплексное число А такое, что для любого e > 0 будет ïD f ( z )/D z - Aï < e как только ïDzï < d (d = d(e) > 0), то функция f называется моногенной в точке z, а число А — её производной в этой точке: А = f' ( z ) = df ( z )/ dz. Функция, моногенная в каждой точке области D, называется моногенной в области D.

Если функция f моногенна в точке z Î D, то f и соответствующие функции j и y имеют в этой точке частные производные по х и y; при этом ¶ f /¶ x = ¶y/¶x + i (¶y/¶x), ¶ f /¶y = ¶j/¶y + i (¶y/¶y) . Производную f’ ( z ) мо жно выразить через частные производные f по х и по у (достаточно вычислить предел отношения D f ( z )/D z двумя разными способами — при D z = Dx ® 0 и при D z = i D y ® 0; приравнивая соответствующие выражения, получаем ¶ f /¶ x = (1/ i )¶ f /¶ y или, что то же самое, ¶ f /¶ x + i(¶ f /¶ y ) = 0. Переходя к функциям j и y, это равенство можно переписать так: ¶j/¶ x = ¶y/¶ y , ¶j/¶ y = — ¶y/¶ x . Если функция f моногенна в области D, то последние соотношения справедливы в каждой точке области D; они называются уравнениями Коши — Римана. Следует отметить, что эти уравнения встречались уже в 18 в. в связи с изучением функций комплексного переменного в трудах Д'Аламбера и Л. Эйлера.

Моногенность функции f эквивалентна её дифференцируемости в смысле комплексного анализа. При этом под дифференцируемостыо f в точке z Î D понимается возможность представления её приращения в виде D f ( z ) = A D z + a(D z )D z , где a(Dz) ® 0 при D z ® 0; дифференциал df ( z ) функции f в точке z, равный главной части A D z её приращения D f ( z ), в этом случае пропорционален dz = D z и имеет вид f’ ( z ) dz. Полезно сравнить понятия дифференцируемости функции f — в смысле действительного анализа и в смысле комплексного анализа. В первом случае дифференциал df имеет вид (¶ f /¶ x ) dx + (¶ f /¶ y ) dy. Удобно переписать это выражение в комплексной форме. Для этого переходят от независимых переменных x, у к переменным z , 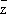, которые формально можно считать новыми независимыми переменными, связанными со старыми соотношениями: z = х + iy, 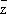= x - iy (становясь на эту точку зрения, функцию f иногда записывают в виде f (z, 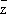) . Выражая dx и dy через dz и d 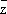по обычным правилам вычисления дифференциалов, получают df = (¶ f/ ¶ z ) dz + (¶ f/ ¶ 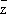) d 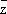, где ¶f/¶z = ( 1/ 2) (¶f/¶x - i¶f/¶y) и ¶f/¶ 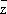= ( 1/ 2) (¶f/¶x + i¶f/¶y) (формальные) производные функции f по z и 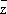соответственно.

Отсюда уже нетрудно заключить, что дифференцируемость функции f в смысле комплексного анализа имеет место в том и только том случае, когда она дифференцируема в смысле действительного анализа и справедливо равенство ¶f/¶ 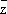= 0 , являющееся краткой формой записи уравнений Коши — Римана; при этом