БСЭ БСЭ - Большая Советская Энциклопедия (АР)

Словесный порядковый счёт (раз, два, три и т.д.), прямую зависимость которого от пальцевого счёта (последовательное произнесение названий пальцев, частей рук) в некоторых случаях можно проследить непосредственно, связывается в дальнейшем со счётом групп, содержащих определённое число предметов. Это число образует основание соответствующей системы счисления, обычно, в результате счёта по пальцам двух рук, равное 10. Встречаются, однако, и группировки по 5, по 20 (французское 80 «quatre-vingt» = 4 ´ 20), по 40, по 12 («дюжина»), по 60 и даже по 11 (Новая Зеландия). В эпоху развитых торговых сношений способы нумерации (как устной, так и письменной) естественно обнаруживали тенденцию к единообразию у общавшихся между собой племён и народностей; это обстоятельство сыграло решающую роль в установлении и распространении применяемой в наст. время системы нумерации ( счисления ), принципа поместного (поразрядного) значения цифр и способов выполнения арифметических действий. По-видимому, аналогичными причинами объясняется и общеизвестное сходство имён числительных в различных языках: например, два — dva (санскр.), duo (греч.), duo (лат.), two (англ.).

Источником первых достоверных сведений о состоянии арифметических знаний в эпоху древних цивилизаций являются письменные документы Др. Египта ( папирусы математические ), написанные приблизительно за 2 тыс. лет до н. э. Это — сборники задач с указанием их решений, правил действий над целыми числами и дробями со вспомогательными таблицами, без каких бы то ни было пояснений теоретического характера. Решение некоторых задач в этом сборнике производится, по существу, с помощью составления и решения уравнений; встречаются также арифметические и геометрические прогрессии.

О довольно высоком уровне арифметической культуры вавилонян за 2—3 тыс. лет до н. э. позволяют судить клинописные математические тексты . Письменная нумерация вавилонян в клинописных текстах представляет собой своеобразное соединение десятичной системы (для чисел, меньших 60) с шестидесятиричной, с разрядными единицами 60, 60 2и т.д. Наиболее существенным показателем высокого уровня А. является употребление шестидесятиричных дробей с распространением на них той же системы нумерации, аналогично современным десятичным дробям. Техника выполнения арифметических действий у вавилонян, в теоретическом отношении аналогичная обычным приёмам в десятичной системе, осложнялась необходимостью прибегать к обширным таблицам умножения (для чисел от 1 до 59). В сохранившихся клинописных материалах, представлявших собой, по-видимому, учебные пособия, находятся, кроме того, и соответствующие таблицы обратных чисел (двузначные и трёхзначные, т. е. с точностью до 1/ 60 2и 1/ 60 3), применявшихся при делении.

У древних греков практическая сторона А. не получила дальнейшего развития; применявшаяся ими система письменной нумерации с помощью букв алфавита была значительно менее приспособлена для производства сложных вычислений, нежели вавилонская (показательно, в частности, что древнегреческие астрономы предпочитали пользоваться шестидесятиричной системой). С другой стороны, древнегреческие математики положили начало теоретической разработке А. в части, касавшейся учения о натуральных числах, теории пропорций, измерения величин и — в неявной форме — также и теории иррациональных чисел. В «Началах» Евклида (3 в. до н. э.) имеются сохранившие своё значение и до сих пор доказательство бесконечности числа простых чисел, основные теоремы о делимости, алгоритмы для нахождения общей меры двух отрезков и общего наибольшего делителя двух чисел (см. Евклида алгоритм ), доказательство несуществования рационального числа, квадрат которого равен 2 (иррациональность числа 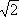), и изложенная в геометрической форме теория пропорций. К рассматривавшимся теоретико-числовым задачам относятся задачи о совершенных числах (Евклид), о пифагоровых числах , а также — уже в более позднюю эпоху — алгоритм для выделения простых чисел ( Эратосфена решето ) и решение ряда неопределённых уравнений 2-й и более высоких степеней (Диофант).

Существенную роль в образовании понятия бесконечного натурального ряда чисел сыграл «Псаммит» Архимеда (3 в. до н. э.), в котором доказывается возможность именовать и обозначать сколь угодно большие числа. Сочинения Архимеда свидетельствуют о довольно высоком искусстве в получении приближённых значений искомых величин: извлечение корня из многозначных чисел, нахождение рациональных приближений для иррациональных чисел, например

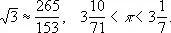
Римляне не продвинули вперёд технику вычислений, оставив, однако, дошедшую до нашего времени систему нумерации ( римские цифры ), мало приспособленную для производства действий и применяемую в настоящее время почти исключительно для обозначения порядковых чисел.

Трудно проследить преемственность в развитии математики в отношении предыдущих, более древних, культур; однако чрезвычайно важные этапы в развитии А. связываются с культурой Индии, оказавшей влияние как на страны Передней Азии и Европы, так и на страны Вост. Азии (Китай, Япония). Помимо применения алгебры к решению задач арифметического содержания, наиболее существенная заслуга индийцев — введение позиционной системы счисления (с применением десяти цифр, включая нуль для обозначения отсутствия единиц в каком-либо из разрядов), сделавшей возможной разработку сравнительно простых правил выполнения основных арифметических действий.

Учёные средневекового Востока не только сохранили в переводах наследие древнегреческих математиков, но и содействовали распространению и дальнейшему развитию достижений индийцев. Методы выполнения арифметических действий, в значительной части ещё далёкие от современных, но уже использующие преимущества позиционной системы счисления, с 10 в. н. э. стали постепенно проникать в Европу, раньше всего в Италию и Испанию.

Сравнительно медленный прогресс А. в средние века сменяется к началу 17 в. быстрым усовершенствованием приёмов вычисления в связи с возросшими практическими запросами к технике вычислений (задачи мореходной астрономии, механики, усложнившиеся коммерческие расчёты и т.п.). Дроби со знаменателем 10, употреблявшиеся ещё индийцами (при извлечении квадратных корней) и неоднократно обращавшие на себя внимание и европейских учёных, применялись сначала в неявной форме в тригонометрических таблицах (в форме целых чисел, выражающих длины линий синуса, тангенса и т.д. при радиусе, принятом за 10 5). Впервые (1427) подробно описал систему десятичных дробей и правила действий над ними аль- Каши . Запись десятичных дробей, по существу совпадающая с современной, встречается в сочинениях С. Стевина в 1585 и с этого времени получает повсеместное распространение. К той же эпохе относится изобретение логарифмов в начале 17 в. Дж. Непером . В начале 18 в. приёмы выполнения и записи вычислений приобретают современную форму.