БСЭ БСЭ - Большая Советская Энциклопедия (АС)

Аси'мптота(от греч. asymptotos — несовпадающий) кривой с бесконечной ветвью, прямая, к которой эта ветвь неограниченно приближается. Например, у гиперболыу = 1/ х ( рис. 1 ) асимптотами являются оси координат Ox и Оу. Кривая может пересекать свою А. (например, график затухающих колебаний, рис. 2 ). Кривые с бесконечными ветвями могут не иметь А. (например, у параболы нет. А.). Понятие А. играет важную роль в математическом анализе. Так, если график функции y = f ( x ) имеет А., определяемую уравнением у = ах + b, то эта функция может быть представлена в виде f ( x ) = ax + b + a ( x ) , где a ( х ) ® 0 при х ® ¥.

Э. Г. Позняк.

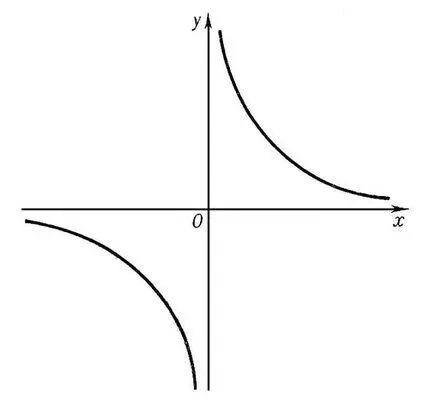
Рис. 1 к статье Асимптота.

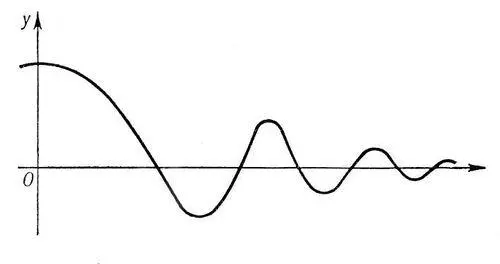
Рис. 2 к статье Асимптота.

Асимптоти'ческая то'чкакривой, см. Особая точка.

Асимптоти'ческая усто'йчивость,см. Устойчивость системы автоматического управления.

Асимптоти'ческое выраже'ние,сравнительно простая элементарная функция, приближённо равная (с как угодно малой относительной погрешностью) более сложной функции при больших значениях аргумента (или при значениях аргумента, близких к данному значению, например нулю); А. в. иногда называется также асимптотической формулой или оценкой. Точное определение: функция j ( x ) является А. в. для f ( x ) при х ® ¥ (или х ® а ) , если f ( x ) /j ( x ) ® 1 при х ® ¥ (или х ® а ) , или, что то же самое, если f ( x ) = j ( x )[1 + a ( x )] , где a ( х ) ® 0 при х ® ¥ (или х ® а ) . В этом случае пишут: f ( x ) ~ j ( x ) при х ® ¥ (или х ® а ) . Как правило, j (x) должна быть легко вычислимой функцией. Простейшими примерами А. в. при х ® 0 могут служить sin x ~ x, tg x ~ x, ctg x ~ 1 /x, 1 - cos x ~ x 22, ln(1 + x ) ~ x, a x- 1 ~ x ln a (a > 0, a ¹ 1). Более сложные А. в. при х ® ¥ возникают для важных функций из теории чисел и специальных функций математической физики. Например, p( x ) ~ x/ ln х, где p( x ) — число простых чисел, не превосходящих х,

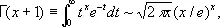
где Г( u ) — гамма-функция, для целочисленных значений х = n имеем Г(n + 1) = n !, что приводит к Стирлинга формуле:

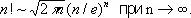
Ещё более сложными А. в. обладают, например, Бесселя функции.

А. в. рассматриваются также в комплексной плоскости z = x + iy. Так, например, \sin ( x + iy ) \ ~ e /y//2 при y ® ¥ и y ® -¥.

А. в. является, вообще говоря, частным случаем (главным членом) более сложных (и точных) приближённых выражений, называемых асимптотическими рядами, или разложениями.

Лит.: де Брёйн Н. Г., Асимптотические методы в анализе, пер. с англ., М., 1961; Евграфов М. А., Асимптотические оценки и целые функции, 2 изд., М., 1962.

В. И. Левин.

А'сино,город (до 1952 — посёлок), центр Асиновского района Томской области РСФСР, на левобережье р. Чулым (приток Оби). Конечная станция ж.-д. линии, идущей от Сибирской магистрали через Томск. 30 тыс. жит. (1968). Строится (1970) ж. д. от А. на Белый Яр. Крупная перевалка леса с р. Чулым на ж. д. Деревообрабатывающий комбинат. Производство стандартных домов.

Асинхро'нная вычисли'тельная маши'на(от греч. а — отрицательная частица и synchronos — одновременный), ЦВМ, в которой начало выполнения каждой операции определяется сигналом окончания предыдущей операции. А. в. м. обладают переменным рабочим тактом, величина которого зависит от длительности операции. Асинхронный принцип обеспечивает машине сравнительно большую скорость вычислений и позволяет достаточно просто согласовать работу устройств с различным быстродействием. Кроме того, он создаёт некоторый самоконтроль машины, поскольку в случае невыполнения какой-либо операции или неполучения сигнала о её окончании машина останавливается. А. в. м. могут быть частично асинхронными — асинхронный принцип применяется лишь для выполнения тех операций, продолжительность которых существенно больше времени обращения к оперативному запоминающему устройству (например, умножение, деление, ввод информации и т.д.), а остальные операции имеют постоянный такт работы (см. Цифровая вычислительная машина ) .

Асинхро'нная му'фта,электромагнитная муфта скольжения для плавного регулирования частоты вращения приводимого механизма при практически постоянной частоте вращения электродвигателя. А. м. состоит из ведомой части — ротора асинхронной электрической машины (чаще с короткозамкнутой обмоткой), и ведущей наружной части с явно выраженными полюсами, возбуждаемыми постоянным током от постороннего источника. При вращении ведомая часть муфты отстаёт от ведущей; при этом вследствие электромагнитной индукции возникает вращающий момент, увлекающий ведомую часть аналогично тому, как вращающееся магнитное поле асинхронного электродвигателя увлекает за собой ротор. Изменением силы тока возбуждения можно регулировать частоту вращения ведомой части муфты в широких пределах. А. м. применяют в электроприводах судовых движителей, в аэродинамических трубах и др.

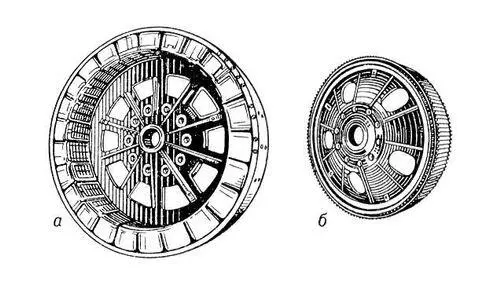
Асинхронная муфта с внутренним расположением ротора:а — ведущая часть (индуктор); б — ведомая часть (ротор) с короткозамкнутой обмоткой..

Асинхро'нная электри'ческая маши'на,электрическая машина переменного тока, у которой частота вращения ротора не равна частоте вращения магнитного поля статора (см. Вращающееся магнитное поле ) . А. э. м. в основном служат двигателями и сравнительно редко генераторами (см. Асинхронный электродвигатель, Асинхронный генератор ) . А. э. м. может также работать в режиме тормоза, если её ротор вращать против направления вращения магнитного поля; это свойство А. э. м. используется, например, в системах электрической тяги на переменном токе.