БСЭ БСЭ - Большая Советская Энциклопедия (ВА)

Лит.: К. F. W. Wander, 1803 bis 1879, В. 1954.

А. И. Пискунов.

Ва'ндербейлпарк,город в ЮАР; см. Фандербейлпарк .

Ван-дер-Ва'альсЯн Дидерик, голландский физик; см. Ваальс Я. Д. ван дер.

Ван-дер-Ва'альса уравне'ние,одно из первых уравнений состояния реального газа, предложенное голландским физиком Я. Д. Ван-дер-Ваальсом (1873):

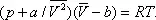
Здесь: р — давление газа; Т — его температура; 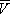— объём одного моля вещества; R — универсальная газовая постоянная ; а и b — константы, учитывающие отклонение свойств реального газа от свойств идеального. Член 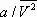, имеющий размерность давления, учитывает притяжение между молекулами газа за счёт ван-дер-ваальсовых сил (см. Межмолекулярное взаимодействие ). Константа b является поправкой на собственный объём молекул газа и учитывает отталкивание молекул на близких расстояниях. Константы а и b обычно определяются из экспериментальных данных. При больших 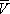можно пренебречь обеими поправками и В. у. переходит в уравнение состояния идеального газа (см. Клапейрона уравнение ).

В. у. является приближённым и количественно описывает свойства реальных газов лишь в области высоких температур и низких давлений. Однако качественно оно позволяет описывать поведение газа при высоких давлениях, конденсацию газа в жидкость и критическое состояние (см. также Уравнение состояния ).

На рис. изображено семейство изотерм (кривых зависимости р от 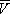при постоянной температуре), рассчитанных по В. у. Это уравнение, кубическое относительно 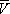, имеет три корня. При низких температурах все три корня — действительные, а выше определённой температуры Тк , называемой критической, остаётся лишь один действительный корень. Физически это означает, что при Т > Т к вещество может находиться лишь в одном (газообразном) состоянии, а ниже Т к — в трёх состояниях (двух стабильных — жидком 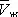и газообразном 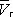— и одном нестабильном). Графически это выражается так: при Т < Т к изотерма имеет три точки пересечения с прямой ac , параллельной оси объёмов. Точки прямой ac отвечают равновесию жидкости и её насыщенного пара. В условиях равновесия, например в состоянии, соответствующем точке b , относительные количества жидкости и пара определяются отношением отрезков bc / ba («правило моментов»). Равновесию фаз при определённой температуре соответствуют давление насыщенного пара р нп и интервал объёмов от 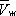до 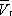. При более низких давлениях (правее 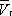) изотерма характеризует свойства газа. Левая, почти вертикальная часть изотермы отражает очень малую сжимаемость жидкости. Участки ad и ес относятся соответственно к перегретой жидкости и переохлажденному пару ( метастабильные состояния ). Участок de физически неосуществим, так как здесь происходит увеличение объёма при увеличении давления. Совокупность точек а , a' , а» ... и с , c' , с» ... определяет кривую, называемую бинодалью, которая очерчивает область совместного существования газа и жидкости. В критической точке К температура, давление и объём ( Тк , р к , 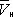) имеют значения, характерные для каждого вещества. Однако, если в В. у. ввести относительные величины: Т/Т к , Р/р к и 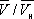, то можно получить так называемое приведённое В. у., которое является универсальным, то есть не зависит от индивидуальных свойств вещества.

Лит.: Штрауф Е. А., Молекулярная физика, Л. — М., 1949; 3оммерфельд А., Термодинамика и статистическая физика, пер. с нем., М., 1955: Вукалович М. П. и Новиков И. И., Уравнение состояния реальных газов, М. — Л., 1948.

А. А. Лопаткин.

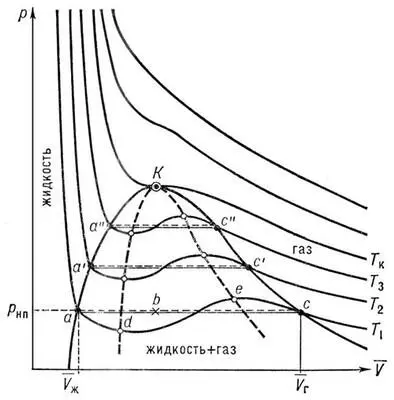
Диаграмма состояния вещества в координатах объем — давление ( 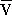, p): Т 1, Т 2, Т 3, Т к— изотермы, рассчитаные по уравнению Ван-дер-Ваальса; К — критическая точка. Линия dke («спинодаль») очерчивает область неустойчивых состояний.

Ван-дер-Ва'альсовы си'лы,распространённое название сил межмолекулярного взаимодействия .

Ван-дер-Ва'рденБартел Лендерт, математик; см. Варден Б. Л. ван дер.

Вандерве'льде(Vandervelde) Эмиль (25.1.1866, Иксель, — 27.12.1938, Брюссель), бельгийский политический деятель, правый социалист, один из лидеров 2-го Интернационала. По образованию юрист. Профессор политэкономии Брюссельского университета (1924). Член Бельгийской социалистической партии с момента её основания (1885), с середины 90-х гг. 19 в. её руководитель. С 1894 член палаты депутатов. С 1900 председатель Международного социалистического бюро 2-го Интернационала. Во время 1-й мировой войны социал-шовинист; в 1914 вошёл в буржуазное правительство и до 1937 неоднократно занимал посты министра иностранных дел, юстиции и др. После Февральской революции 1917 В. приезжал в Россию для агитации за продолжение империалистической войны. Был представителем Бельгии на Парижской мирной конференции 1919—20 и подписал Версальский мирный договор 1919 . В 1922 присутствовал на процессе правых эсеров в Москве в качестве защитника. Будучи в 1925—27 министром иностранных дел, подписал Локарнские соглашения 1925. Автор книг и брошюр, написанных с оппортунистических позиций; выступал против признания СССР, оправдывал колониальную политику Бельгии в Конго.

Соч.: Le Parti ouvrier beige 1885—1925, Brux., 1925.

Лит.: Ленин В. И., Оппортунизм и крах II Интернационала, Полн. собр. соч., 5 изд., т. 27; его же. Пролетарская революция и ренегат Каутский, там же, т. 37, с. 332—338.