БСЭ БСЭ - Большая Советская Энциклопедия (ГА)

3) Снасть, крепящая к мачте нижний наветренный угол паруса (галсовый угол).

Галса'новЦэдэн (Цыденжап) Галсанович [р. 10(23).2.1917, улус Илька, ныне Заиграевский аймак Бурят. АССР], бурятский советский поэт. Член КПСС с 1962. Печатается с 1931. Автор поэм «Четыре дня и три ночи» (1939), «Соревнование на мудрость» (1940), «Эхо на Чудском озере» (1943), «Павел Балтахинов» (1945) — о народном герое, «Поэма о пятилетке» (1947), «Мои весёлые друзья» (1962): сборников стихов «Байкальские волны» (1940), «Советское солнце» (1951), «Мы молоды» (1959) и др. Творчество Г. посвящено теме дружбы и единства советских народов и их трудовым подвигам. Переводил на бурятский язык произведения А. С. Пушкина, А. С. Грибоедова, Н. А. Некрасова, В. В. Маяковского. Награжден орденом «Знак Почёта» и медалями.

Соч.: Шэлэтдэмэл зохёолнууд, Улан-Удэ, 1948; Дуунайм дээжэ, Улан-Удэ, 1962; в рус. пер. — Избр. произведения. Стихи и поэмы, Улан-Удэ, 1948; Байкальские стихи, М., 1960.

Лит.: Хамаганов М. П., Основные черты творчества Цэдэна Галсанова,Улан-Удэ, 1948; Писатели Советской Бурятии. Биобиблиографический справочник, Улан-Удэ, 1959; История бурятской советской литературы, Улан-Удэ. 1967.

Га'лстушник(Charadrius hiaticula), кулик рода ржанок.

Галте'ль(от нем. Hohikehie), профилированная рейка (брусок, планка), служащая для прикрытия щелей в стыках соединений (например, между полом и стеной), выступающих рёбер и краев (например, в мебели) и т. д. Под Г. понимают также скругление внешних и внутренних углов на деталях машин, в литейных формах и т. п. Г. облегчают изготовление и обработку деталей, предупреждают возникновение трещин в местах сопряжений.

Галто'вка,процесс очистки поверхности небольших заготовок и деталей от заусенцев, окалины, формовочной земли, коррозии и др. Служит также для улучшения качества поверхности изделий — полирования. Г. осуществляется в барабанах. Для ускорения Г. в барабан вместе с деталями загружают абразивные материалы — песок, наждак, корунд и др (сухая Г.), а иногда заливают различные растворители (мокрая Г.). Для полирования в барабаны вместе с деталями загружают деревянные опилки, обрезки кожи и др. (сухое полирование), иногда вводят растворы мыла, щёлочи и др. (мокрое полирование). Для лучшего перемешивания применяют барабаны с эксцентричным вращением.

При виброгалтовке рабочим камерам сообщают колебания в нескольких направлениях с частотой от 15 до 50 гц, что обеспечивает сложное перемещение деталей и абразивных частиц. Виброгалтовка позволяет обрабатывать крупные детали (в закрепленном виде).

Применяют также гидрогалтовку, при которой создаётся поверхностный наклёп, повышающий усталостную прочность материала детали. При гидрогалтовке детали закрепляются в камере, внутри, которой движется жидкость с мелкой металлической дробью.

Д. И. Браславский, В. М. Раскатов.

Галуа' тео'рия,созданная Э. Галуа теория алгебраических уравнений высших степеней с одним неизвестным, т. е. уравнений вида

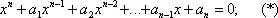
устанавливает условия сводимости решения таких уравнений к решению цепи др. алгебраических уравнений (обычно более низких степеней). Т. к. решением двучленного уравнения x m = А является радикал 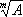, то уравнение (*) решается в радикалах, если его можно свести к цепи двучленных уравнений. Все уравнения 2-й, 3-й и 4-й степеней решаются в радикалах. Уравнение 2-й степени x 2+ px + q = 0 было решено в глубокой древности по общеизвестной формуле

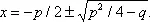
уравнения 3-й и 4-й степеней были решены в 16 в. Для уравнения 3-й степени вида x 3+ px + q = 0 (к которому можно привести всякое уравнение 3-й степени) решение даётся т. н. формулой Кардано:

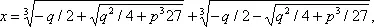
опубликованной Дж. Кардано в 1545, хотя вопрос о том, найдена ли она им самим или же заимствована у др. математиков, нельзя считать вполне решенным. Метод решения в радикалах уравнений 4-й степени был указан Л. Феррари.

В течение трёх последующих столетий математики пытались найти аналогичные формулы для уравнений 5-й и высших степеней. Наиболее упорно над этим работали Э. Безу и Ж. Лагранж. Последний рассматривал особые линейные комбинации корней (т. н резольвенты Лагранжа), а также изучал вопрос о том, каким уравнениям удовлетворяют рациональные функции от корней уравнения (*). В 1801 К. Гаусс создал полную теорию решения в радикалах двучленного уравнения вида x n = 1, в которой свёл решение такого уравнения к решению цепи двучленных же уравнений низших степеней и дал условия, необходимые и достаточные для того, чтобы уравнение x n = 1 решалось в квадратных радикалах. С точки зрения геометрии, последняя задача заключалась в отыскании правильных n-угольников, которые можно построить при помощи циркуля и линейки; поэтому уравнение x n = 1 и называется уравнением деления круга. Наконец, в 1824 Н. Абель показал, что общее уравнение 5-й степени (и тем более общие уравнения высших степеней) не решается в радикалах. С другой стороны, Абель дал решение в радикалах одного общего класса уравнений, содержащего уравнения произвольно высоких степеней, т. н. абелевых уравнений.

Т. о., когда Галуа начал свои исследования, в теории алгебраических уравнений было сделано уже много, но общей теории, охватывающей все возможные уравнения вида (*), ещё не было создано. Например, оставалось: 1) установить необходимые и достаточные условия, которым должно удовлетворять уравнение (*) для того, чтобы оно решалось в радикалах; 2) узнать вообще, к цепи каких более простых уравнений, хотя бы и не двучленных, может быть сведено решение заданного уравнения (*) и, в частности, 3) выяснить, каковы необходимые и достаточные условия для того, чтобы уравнение (*) сводилось к цепи квадратных уравнений (т. е. чтобы корни уравнения можно было построить геометрически с помощью циркуля и линейки). Все эти вопросы Галуа решил в своём «Мемуаре об условиях разрешимости уравнений в радикалах», найденном в его бумагах после смерти и впервые опубликованном Ж. Лиувиллем в 1846. Для решения этих вопросов Галуа исследовал глубокие связи между свойствами уравнений и групп подстановок, введя ряд фундаментальных понятий теории групп. Своё условие разрешимости уравнения (*) в радикалах Галуа формулировал в терминах теории групп. Г. т. после Галуа развивалась и обобщалась во многих направлениях. В современном понимании Г. т. — теория, изучающая те или иные математические объекты на основе их групп автоморфизмов (так, например, возможны Г. т. полей, Г. т. колец, Г. т. топологических пространств и т. п.).