БСЭ БСЭ - Большая Советская Энциклопедия (ГА)
- Название:Большая Советская Энциклопедия (ГА)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (ГА) краткое содержание
Большая Советская Энциклопедия (ГА) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Для решения задач Дирихле, Неймана и др. краевых задач теории Г. ф. разработаны различные методы, имеющие большое теоретическое значение. Например, для задачи Дирихле известны: альтернирующий метод (Шварца), метод выметания (Пуанкаре), метод интегральных уравнений (Фредгольма), метод верхних и нижних функций (Перрона) и др. При рассмотрении краевых задач для областей общего вида возникают важные вопросы об условиях существования решений, об устойчивости решений при малых изменениях границы области и др. Этим вопросам посвящены работы М. В. Келдыша, М. А. Лаврентьева и др. советских математиков. Весьма большое значение для приложений теории Г. ф. к задачам физики и техники имеет также разработка методов численного решения краевых задач.
Лит.: Келдыш М. В., О разрешимости и устойчивости задачи Дирихле, «Успехи математических наук», 1940, в. 8; Сретенский Л. Н., Теория ньютоновского потенциала, М.—Л., 1946; Смирнов В. И., Курс высшей математики, 3 изд., т. 4, М., 1957; Петровский И. Г., Лекции об уравнениях с частными производными, 3 изд., М., 1961.
А. И. Маркушевич.
Гармонический анализ
Гармони'ческий ана'лиз, отдел математики, связанный с разложением колебаний на гармонические колебания . При изучении периодических (т. е. повторяющихся во времени) явлений рассматриваются периодические функции . Например, гармоническое колебание описывается периодической функцией времени t ::
A sin ( wt + j ), называется гармоникой. Основная задача Г. а. состоит в расщеплении периодической функции на простейшие гармонические составляющие, т. е. в представлении периодической функции в виде тригонометрического ряда (см. Фурье ряд ).
Гармонический анализатор
Гармони'ческий анализа'тор, вычислительное устройство для нахождения амплитуд гармоник сложных периодических функций . Применяются при динамических исследованиях кривошипно-шатунных механизмов двигателей, для предварительной оценки влияния внешних периодических воздействий на колебательную систему, анализа звуковых колебаний и решения аналогичных задач. В состав практически всех типов Г. а. входят устройство ввода, перемножающие устройства , интегрирующие устройства . Основными характеристиками Г. а. (по которым они и классифицируются) являются: вид задаваемой функции (график, электрический сигнал, механическое перемещение), наибольший номер гармоники, количество одновременно вычисляемых коэффициентов. Наиболее широко распространены механические Г. а., при помощи которых, вручную обводя график заданной функции, можно получить одновременно значения амплитуд 20—25 гармоник.
Лит.: Басманов В. В., Вычислительные математические приборы, М.. 1958; Мейер цур Капеллен В., Инструментальная математика для инженеров, пер. с нем, М., 1959.
Гармонический баланс
Гармони'ческий бала'нс, принцип гармонического баланса, принцип эквивалентной линеаризации нелинейностей, основанный на условном отождествлении данного нелинейного элемента с некоторым линейным элементом, установившаяся реакция которого на гармоническое воздействие совпадает с первой гармоникой реакции на то же воздействие исходного нелинейного элемента. Параметры эквивалентного линейного элемента зависят от амплитуды гармонического воздействия.
Гармонический ряд
Гармони'ческий ряд, числовой ряд
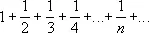
Каждый член Г. р. (начиная со 2-го) является гармоническим средним между двумя соседними (отсюда название — Г. р.). Члены Г. р. стремятся к нулю, однако Г. р. расходится (Г. Лейбниц , 1673). Сумма n первых членов Г. р. имеет следующее асимптотическое выражение (Л. Эйлер , 1740):
S n = ln n + С+ e n,
где С = 0,577215... — Эйлера постоянная , а e n ® 0 при n ® ¥.
Гармонический синтезатор
Гармони'ческий синтеза'тор, специализированное вычислительное устройство для получения сложной функции, образуемой суммированием кратных по частоте и различных по амплитуде и фазе простых синусоидальных функций. Применяется главным образом в лабораторных исследованиях для анализа сложных систем со многими источниками колебаний. Г. с. различаются по количеству суммируемых синусоид и максимальным значениям их амплитуд.
Гармоническое расположение
Гармони'ческое расположе'ние, такое расположение четырёх точек M 1, М 2, М 3, М 4 на прямой ll 1 (см. рис. ), при котором точка М 3 лежит внутри отрезка M 1M 2 , точка М 4 — вне этого отрезка и отношения
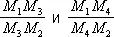
равны.
Обычно отношение двух отрезков считают положительным, если их направления на прямой одинаковы, и отрицательным при различных направлениях. Поэтому Г. р. точек M 1, M 2, М 3, М 4 можно охарактеризовать и тем, что т. н. двойное отношение этих точек, т. е. отношение
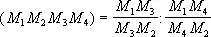
равно -1.
Гармонически расположенные точки при проектировании на какую-нибудь прямую переходят в гармонически расположенные точки. Поэтому Г. р. есть одно из основных понятий проективной геометрии. Г. р. точек M 1, M 2, M 3, M 4 связано со следующей геометрической конфигурацией. Пусть точки M 1 и M 2 являются точками пересечения попарно противоположных сторон четырёхугольника ABCD , тогда точки M 3 и M 4 будут точками пересечения диагоналей этого четырёхугольника с прямой M 1 , M 2 .
Понятие Г. р. переносится и на др. геометрические объекты: четыре луча, проектирующие из одной точки гармонически расположенные точки, образуют гармонический пучок лучей. Аналогично определяется гармонический пучок плоскостей.
Э. Г. Позняк.
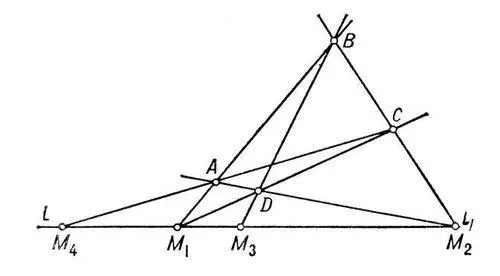
Рис. к ст. Гармоническое расположение.
Гармоническое среднее
Гармони'ческое сре'днее,число ( у ), обратное которому есть арифметическое среднее чисел, обратных данным числам ( а 1, a 2,..., a n ):
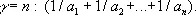
Гармония (музык.)
Гармо'ния,выразительные средства музыки, основанные на объединении музыкальных звуков в созвучия и последованиях созвучий в условиях лада и тональности. Важнейшее значение в Г. имеют аккорды— созвучия, звуки которых расположены или могут быть расположены по терциям. Терцовое построение аккордов опирается на естественные акустические предпосылки, в первую очередь на натуральный звукоряд (порой применяются и др. принципы построения аккордов, например квартовый). В последованиях аккордов выявляются их ладовые функции (см. Функции ладовые ) -, некоторые воспринимаются как устойчивые (центральный аккорд лада, определяющий тональность, тоника ) , другие — как неустойчивые (группы доминанты и субдоминанты ) . Логика ладофункционального движения сочетается в последованиях аккордов с естественностью движения составляющих их голосов ( голосоведение ) . Аккорды и их последования не только подчиняются ладофункциональным закономерностям, но и обладают своими колористическими (фоническими) качествами. Однако выразительность Г. зависит от всех элементов музыкального языка, и в первую очередь от мелодии. Со своей стороны, Г. влияет на восприятие мелодии (см. Гармонизация ) . Г. участвует в созидании музыкальной формы. В построении различных форм существенно значение многих гармонических средств, например каденций, модуляций, соотношения и последования тональностей.
Читать дальшеИнтервал:
Закладка:
