БСЭ БСЭ - Большая Советская Энциклопедия (ВО)

где F i — действующие активные силы, d s i— величины возможных перемещений точек приложения этих сил, α i — углы между направлениями сил и возможных перемещений. Для систем с несколькими степенями свободы уравнение (1) должно составляться для каждого независимого перемещения в отдельности.

Таким образом, В. п. п. позволяет найти условия равновесия системы, не вводя неизвестных реакций связей, что существенно упрощает решение и расширяет класс разрешимых задач. Например, с помощью В. п. п. легко найти условия равновесия подъёмного механизма, детали которого скрыты в коробке К (см. рис .). Из уравнения (1) получаем

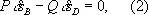
где Р и Q — действующие силы. Для окончательного расчёта надо установить зависимость между перемещениями d s B и d s D. Если при одном повороте рукоятки АВ винт поднимается на величину h, то эта зависимость найдётся из пропорции d s B : d s D = 2p a : h , где а — длина рукоятки. Окончательно уравнение (2) даёт следующее условие равновесия Р = Qh/ 2p a . Методами геометрической статики (если скрытые в коробке детали механизма неизвестны) эта задача вообще решена быть не может.

О применении аналогичного метода к решению задач динамики см. Д'Аламбера — Лагранжа принцип .

С. М. Тарг.

Рисунок к ст. Возможных перемещений принцип.

Возмуща'ющее возде'йствие,помехи и сигналы, нарушающие функциональную связь между задающим воздействием и регулируемой величиной в системах автоматического управления.

Возмуще'ния магни'тные, см. Вариации магнитные .

Возмуще'ния небе'сных тел,отклонения реальных траекторий небесных тел от траекторий, по которым они двигались бы в случае взаимодействия с одним единственным телом (см. Двух тел задача ). Траектории движения в задаче двух тел представляют собой так называемые конические сечения — эллипс, параболу, гиперболу. Движение по коническому сечению можно рассматривать как первое приближение при условии, что одна из притягивающих масс значительно превосходит по своей величине все остальные. Так, например, в Солнечной системе движение планет вокруг Солнца можно рассматривать, в первом приближении, как движение по эллиптическим орбитам. Взаимные возмущения планет в этом случае малы и могут быть вычислены путём разложений в ряды по степеням малых параметров (аналитические методы) или численным интегрированием уравнений движения (численные методы). За малые параметры принимают обычно массы планет, выраженные в единицах массы Солнца, а также эксцентриситеты и наклоны их орбит. Члены ряда называются возмущениями пли неравенствами в движении небесных тел и имеют вид: At m , где m = 1, 2,..., и A sin (a t + b). Члены первого вида называются вековыми возмущениями, второго вида — периодическими. Коэффициенты А содержат множителем массы планет в различных положительных степенях и потому являются малыми величинами. Возмущения, содержащие массы планет в первой степени, называются возмущениями первого порядка, во второй степени второго порядка и т.д. При построении теории движения больших планет приходится учитывать возмущения второго порядка и некоторые возмущения третьего порядка. Среди периодических возмущений особого внимания требуют те, у которых коэффициент a в аргументе тригонометрической функции очень мал. Так как период возмущения равен 360°/a, то при малом a период соответствующего возмущения очень велик по сравнению с периодом обращения самой планеты вокруг Солнца; такие возмущения называются долгопериодическими.

Причиной возмущений в движении небесных тел, в том числе и искусственных (см. Искусственные спутники Земли ), может быть притяжение других небесных тел, отклонения фигур этих тел от сферической формы, сопротивление среды, в которой происходит движение, изменение массы тела с течением времени, световое давление и т.п. В случае двойных звёзд возмущения вызываются притяжением других близких звёзд, а также общим гравитационным полем галактики. Определение В. н. т. представляет весьма громоздкую задачу в вычислительном отношении. Так, например, в теории движения Луны, предложенной Э. Брауном, солнечные возмущения в формуле, по которой определяется долгота Луны, содержат 312 тригонометрических членов. Для вычисления возмущений по готовым разложениям в ряды, а также и для получения самих тригонометрических рядов по заданным элементам орбит небесных тел с успехом применяются быстродействующие электронные вычислительные машины. При численном интегрировании уравнений движения можно непосредственно получить возмущённые координаты небесных тел, и тогда вопрос о вычислении возмущений отпадает (метод Коуэлла). Теория возмущённого движения небесных тел составляет основное содержание небесной механики .

Лит . см. при ст. Небесная механика .

Г. А. Чеботарёв.

Вознесе'ние,один из 12 «великих» праздников в православной церкви, отмечающийся на 40-й день после пасхи , в честь мифического «вознесения» Христа на небо.

Вознесе'ния О'стров(Ascension Island), в центральной части Атлантического океана (7°57 ' ю. ш., 14°22 ' з. д.). Колония Великобритании. Площадь 88 км 2. Население 434 человека (1965). Административный центр — г. Джорджтаун. Поверхность — вулканическое плато, усеянное кратерами потухших вулканов (около 35). Высота до 875 м . Тропические леса. Обилие морских птиц. Открыт португальцами в 1501 в день праздника вознесения.

Вознесе'нск,город (с 1938), центр Вознесенского района Николаевской области УССР. Пристань на р. Южный Буг. Железнодорожная станция (на линии Кировоград — Одесса). 36 тыс. жителей (1970). Пищевая промышленность (мясокомбинат, маслодельный, плодоконсервный заводы), швейная, мебельная фабрики. С.-х. техникум. Краеведческий музей. Основан в 1795.

Вознесе'нскийАндрей Андреевич (р. 12.5.1933, Москва), русский советский поэт. Окончил Московский архитектурный институт (1957). Выступил со стихами в 1958. Поэма В. «Мастера» (1959) привлекла внимание свежестью языка, убеждённостью в высоком призвании искусства. Сборник «40 лирических отступлений из поэмы „Треугольная груша”» (1962), в основном посвящённый впечатлениям поэта от поездки в США, вызвал критическую дискуссию о «современном стиле», о гражданской позиции художника. Выделяются поэмы В. «Лонжюмо» (1963), посвящённая В. И. Ленину, и «Оза» (1964) — раздумье о человеческой личности в эпоху всеобщего «наступления» техники. Поэзия В. отличается острым чувством современности, динамичностью стиха, усложнённой, часто парадоксальной, ассоциативной образностью «урбанистического» характера, причудливой игрой аллитераций.