БСЭ БСЭ - Большая Советская Энциклопедия (ВТ)

Статистическая физика , построенная на анализе микроскопического механизма явлений, происходящих в макроскопических телах, и выяснившая физическую сущность энтропии, позволила понять природу В. н. т., определить пределы его применимости и устранить кажущееся противоречие между механической обратимостью любого, сколь угодно сложного микроскопического процесса и термодинамической необратимостью процессов в макротелах.

Как показывает статистическая термодинамика (Л. Больцман , Дж. Гиббс ), энтропия системы связана со статистическим весом Р макроскопического состояния:

S = k ln P ( k — Больцмана постоянная ). Статистический вес Р пропорционален числу различных микроскопических реализаций данного состояния макроскопической системы (например, различных распределений значений координат и импульсов молекул газа, отвечающих определённому значению энергии, давления и других термодинамических параметров газа), т. е. характеризует как бы степень неточности микроскопического описания макросостояния. Для замкнутой системы вероятность термодинамическая W данного макросостояния пропорциональна его статистическому весу и определяется энтропией системы:

W ~ exp ( S / k ). (2)

Таким образом, закон возрастания энтропии имеет статистически-вероятностный характер и выражает постоянную тенденцию системы к переходу в более вероятное состояние. Максимально вероятным является состояние равновесия; за достаточно большой промежуток времени любая замкнутая система достигает этого состояния.

Энтропия является величиной аддитивной (см. Аддитивность ), она пропорциональна числу частиц в системе. Поэтому для систем с большим числом частиц даже самое ничтожное относительное изменение энтропии, приходящейся на одну частицу, существенно меняет её абсолютную величину; изменение же энтропии, стоящей в показателе экспоненты в ур-нии (2), приводит к изменению вероятности данного макросостояния W в огромное число раз. Именно этот факт является причиной того, что для системы с большим числом частиц следствия В. н. т. практически имеют не вероятностный, а достоверный характер. Крайне маловероятные процессы, сопровождающиеся сколько-нибудь заметным уменьшением энтропии, требуют столь огромных времён ожидания, что их реализация является практически невозможной. В то же время малые части системы, содержащие небольшое число частиц, испытывают непрерывные флуктуации, сопровождающиеся лишь небольшим абсолютным изменением энтропии. Средние значения частоты и размеров этих флуктуаций являются таким же достоверным следствием статистической термодинамики, как и само В. н. т.

Проиллюстрируем сказанное примером, позволяющим оценить масштабы величин, определяющих точность В. н. т. и отклонения от него. Рассмотрим флуктуационный процесс, в результате которого N частиц, первоначально занимающих объём V , равный 1 мкм 3(т. е. 10 -18 м 3), сконцентрируется самопроизвольно в половине этого объёма. Отношение статистических весов начального (1) и конечного (2) состояний:

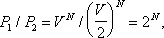
поэтому изменение энтропии D S / k = N in2 и отношение вероятностей W 1/ W 2= 2 N . Если время пролёта частицы через объём V, т. е. время, в течение которого сохраняется данная флуктуация, t = 10 -8 сек , то среднее время ожидания такой флуктуации t =2 N ·t » 10 0,3 N ·t. При числе частиц N = 30, t = 10 сек , при N = 100, t » 10 22 сек » 10 15лет. Если же учесть, что при атмосферное давлении число частиц газа в 1 мкм 3 составляет N ~ 10 8, то время ожидания указанного события

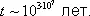
Буквальное применение В. н. т. к Вселенной как целому, приведшее Клаузиуса к неправильному выводу о неизбежности «тепловой смерти Вселенной», является неправомерным, так как любая сколь угодно большая часть Вселенной не является сама по себе замкнутой и её приближение к состоянию теплового равновесия, даже не говоря о флуктуациях, не является абсолютным.

Термодинамическое же описание Вселенной как целого возможно лишь в рамках общей теории относительности, в которой вывод о приближении энтропии к максимуму не имеет места.

И. М. Лифшиц.

Лит.: Планк М., Введение в теоретическую физику, 2 изд., ч. 5, М. — Л., 1935; Френкель Я. И., Статистическая физика, М. — Л., 1948; Ландау Л., Лифшиц Е., Статистическая физика, М. — Л., 1951; Леонтович М. А., Введение в термодинамику, 2 изд., М. — Л., 1952; Самойлович А. Г., Термодинамика и статистическая физика, М., 1953; Смолуховский М., Границы справедливости второго начала термодинамики, «Успехи физических наук», 1967, т. 93, в. 4.

Второ'е се'рбское восста'ние 1815,народное восстание против турецкого гнёта в Сербии, фактически явилось продолжением первого сербского восстания 1804—13 . Началось 11 апреля в Валевской нахии ( Белградский пашалык ). 7 мая повстанцы одержали первую победу над турками у горы Любич близ г. Чачак. 17 мая был освобождён г. Палеж (современный Обреновац) и открыт путь для установления связей с австрийскими сербами, помогавшими повстанцам оружием и снаряжением. 3 июля повстанцы овладели г. Пожаревац. Турки двинули против восставших две армии: из Боснии и из Румелии. Руководитель повстанцев — активный участник восстания 1804—13 — Милош Обренович вынужден был начать переговоры с главнокомандующим турецких армий. Опираясь на дипломатическую поддержку России, он заключил перемирие с румелийским вали Марашлы Али-пашой (28 августа 1815). 10 октября 1815 Милош и Марашлы Али-паша заключили устное соглашение, по которому регламентировались размеры податей спахиям (турецким помещикам), сербы получили право самим собирать налоги султану, сербские кнезы участвовали в суде над сербами наравне с турецкими чиновниками, учреждалась сербская народная канцелярия как высший административный и судебный орган для сербов. Милош стал верховным кнезом Сербии. Несмотря на то что восстание увенчалось лишь частичным успехом, оно создало базу для последующей борьбы за внутреннюю автономию Сербии, завершившуюся в 30-х гг. 19 в. созданием Сербского княжества.

Лит.: История Югославии, т. 1, М., 1963, с. 324—330; Jakшиħ Г. и Страњаковиħ Д., Сербиja од 1813 до 1858 године (Српски народ у XIX веку, књ. 2), Београд, (1937].

В. Г. Карасёв.

Второзако'ние,пятая книга Пятикнижия (составной части Библии ).