БСЭ БСЭ - Большая Советская Энциклопедия (ВЫ)

Простейшими В. т. являются выпуклые многогранники — В. т., ограниченные конечным числом многоугольников. Для любого конечного В. т. можно построить как угодно близкие к нему выпуклые многогранники. Это позволяет решать многие задачи о В. т. следующим образом: задача решается для выпуклых многогранников, а затем путём предельного перехода соответствующий результат обосновывается и для любого В. т. Так, например, определяются площади выпуклых поверхностей и объёмы любых В. т. В частности, устанавливается, что если одно конечное В. т. охватывает другое, то площадь поверхности первого больше площади поверхности второго. Описанный метод был глубоко разработан А. Д. Александровым и применён для решения разнообразных новых задач теории В. т.

Общая теория В. т. и выпуклых поверхностей составляет так называемую геометрию В. т. Задачи геометрии В. т. охватывают широкий круг вопросов: общие свойства В. т. (теоремы об опорных плоскостях, классификация В. т., приближение многогранниками), экстремальные свойства В. т. (например, шар среди всех В. т. с заданным объёмом имеет минимальную поверхность), теоремы о существовании и единственности В. т. с заданными свойствами (например, теорема о существовании выпуклого многогранника с данными направлениями и площадями граней), свойства различных классов В. т. (например, тел постоянной ширины), общие свойства выпуклых поверхностей, теоремы существования и единственности для выпуклых поверхностей, внутренняя геометрия об выпуклых поверхностей и т.д. Понятие В. т. естественно возникает в геометрии пространств постоянной кривизны. Многие перечисленные выше задачи формулируются и решаются для В. т. в таких пространствах. Методы и результаты теории В. т. используются в различных разделах математики: в геометрии, в теории чисел, в математическом анализе. Основы теории В. т. были заложены в конце 19 в. немецким математиками Г. Брунном и Г. Минковским. Важнейшие новые результаты этой теории были получены советскими математиками А. Д. Александровым и А. В. Погореловым.

Лит.: Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М. — Л., 1948; его же, Выпуклые многогранники, М. — Л., 1950; Погорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969.

Э. Г. Позняк.

Рисунок к ст. Выпуклое тело.

Вы'пуклость и во'гнутость,свойство графика функции у = f ( x ) (кривой), заключающееся в том, что каждая дуга кривой лежит не выше (не ниже) своей хорды; в первом случае график функции f ( x ) обращён выпуклостью книзу (вогнутостью кверху) и сама функция называется выпуклой ( рис. 1 , а), во втором — график обращён вогнутостью книзу (выпуклостью кверху) и функция называется вогнутой ( рис. 1 , б). Если существуют производные f ¢( x ) и f ²( х ), то первый случай имеет место при условии, что f ²( x ) ³ 0, а второй при f ²( x ) £ 0 (во всех точках рассматриваемого промежутка). Выпуклость (книзу) можно охарактеризовать также тем, что дуга кривой лежит не ниже касательной, в окрестности любой своей точки ( рис. 2 , a), а вогнутость (книзу) — тем, что дуга кривой лежит не выше касательной ( рис. 2 , б). Аналогично определяются В. и в. поверхности.

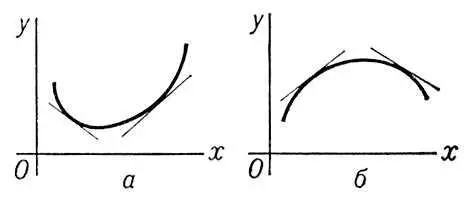
Рис. 2 к ст. Выпуклость и вогнутость.

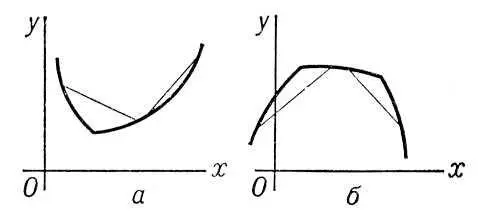
Рис. 1 к ст. Выпуклость и вогнутость.

Вы'пуск руды',перемещение руды из очистного пространства или аккумулирующей ёмкости рудника под действием силы тяжести. В. р. в думпкары, автосамосвалы, на конвейеры осуществляется через так называемые выпускные устройства. На интенсивность этого процесса оказывают влияние влажность и гранулометрический состав руды, а также конструктивные параметры выпускных устройств.

Лит.: Малахов Г. М., Безух В. Р., Петренко П. Д., Теория и практика выпуска обрушенной руды, 2 изд., М., 1968.

Выпь,см. Выпи .

Вы'равненность семя'н,однородность семян по величине (преимущественно по толщине). Семенная партия может иметь высокий вес 1000 семян, но состоять из неоднородных по величине (крупных и мелких) семян, обладающих разными посевными и урожайными качествами. Необходимо, чтобы семена имели высокий вес 1000 штук и хорошую выравненность (не ниже 80% для кондиционных семян), так как от этого зависит равномерное развитие всходов. В. с. зависит от приёмов выращивания семенников, метеорологических факторов, строения соцветий и др. Даже при хорошем развитии растений невыравненность семян сохраняется, что обусловлено расположением их в соцветии. Так, у злаков зерно в средней части колоса более крупное и тяжеловесное, чем в верхних и нижних частях. Особое значение В. с. имеет при гнездовых и пунктирных посевах, поэтому применяют калибровку семян кукурузы и других культур. Очистка и сортирование семян также способствуют их выравненности. В. с. определяют государственные семенные инспекции при контрольно-семенном анализе. Семена разделяют на фракции по размерам, весу, аэродинамическим свойствам, и сумму двух смежных наибольших фракций выражают в процентах к исходной навеске.

М. К. Фирсова.

Выра'вниваниев статистике, метод, при помощи которого получают аналитическое и графическое выражение статистической закономерности, лежащей в основе заданного эмпирического ряда статистических данных. Путём В. ломаную линию уровней эмпирического ряда заменяют плавной «выравнивающей» кривой (в частном случае — прямой) и вычисляют уравнение этой кривой. При В. последовательно решают три задачи: выбирают тип уравнения (форму плавной кривой); вычисляют параметры (коэффициенты) этого уравнения; вычисляют (на основании уравнения) или измеряют (по графику кривой) уровни (ординаты) полученного «теоретического» статистического ряда. Тип уравнения и, соответственно, форму плавной кривой выбирают на основании общих сведений (или часто — из практического опыта) о сущности явления, о закономерностях его структуры и развития, о зависимости между его признаками и т.д. (так называемое «аналитическое» В.); при отсутствии таких предварительных сведений тип уравнения (форму кривой) часто может подсказать графическая форма ломаной, выражающей заданный эмпирический ряд.