БСЭ БСЭ - Большая Советская Энциклопедия (ГР)

Лит.: Лященко П. В., Гравитационные методы обогащения, 2 изд., М. — Л., 1940; Поваров А. И., Гидроциклоны, М,, 1961: Марголин И. З., Обогащение углей и неметаллических ископаемых в тяжёлых суспензиях, М., 1961; Полькин С. И., Обогащение руд и россыпей редких металлов, М., 1967; Акопов М. Г., Основы обогащения углей в гидроциклонах, М., 1967.

В. И. Классен.

Рис. 3. Принципиальная схема гравитационного обогащения угля отсадкой из тяжёлой суспензии.

Рис. 2. Веер частиц разных минералов на поверхности концентрационного стола.

Рис. 1. Сепаратор для гравитационного обогащения угля в тяжёлой суспензии.

Гравитацио'нное по'ле,то же, что поле тяготения; см. Тяготение .

Гравитацио'нное по'ле Земли',поле силы тяжести ; силовое поле, обусловленное притяжением (тяготением) Земли и центробежной силой, вызванной её суточным вращением. Зависит также (незначительно) от притяжения Луны, Солнца и др. небесных тел и масс земной атмосферы. Г. п. З. характеризуется силой тяжести (см. Гравиметрия ), потенциалом силы тяжести и различными производными от него. Потенциал имеет размерность см 2. сек –2. За единицу измерения первых производных потенциала, в том числе силы тяжести, в гравиметрии принимается миллигал ( мгл ), равный 10 –3 см . сек –2, а вторых производных — этвеш ( Е ), равный 10 –9 сек –2. Часть потенциала силы тяжести, обусловленная только притяжением масс Земли, называется потенциалом земного притяжения, или геопотенциалом.

Для решения практических задач потенциал земного притяжения представляется в виде ряда

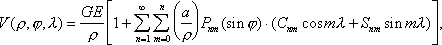
где r — геоцентрическое расстояние; j и l — географическая широта и долгота точки, в которой рассматривается потенциал; P nm — присоединённые функции Лежандра; GE — произведение постоянной тяготения на массу Земли, равное 398 603·10 9 м 3 сек –2, а — большая полуось Земли; C nmи S nm — безразмерные коэффициенты, зависящие от фигуры Земли и внутреннего распределения масс в ней. Главный член ряда — 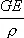соответствует потенциалу притяжения шара с массой Земли. Второй по величине член (содержащий C 20) учитывает сжатие Земли. Последующие члены, коэффициенты которых на три порядка и более меньше, чем C 20, отражают детали фигуры и строения Земли. Из-за отсутствия точных данных об истинном распределении масс внутри Земли и о её фигуре невозможно непосредственно вычислить коэффициенты C nmи S nm. Поэтому они определяются косвенно по совокупности измерений силы тяжести на поверхности Земли и по наблюдениям возмущений в движении близких искусственных спутников Земли (ИСЗ). В табл. приведены результаты определения коэффициентов разложения, установленные на основе наблюдений движения ИСЗ. Аналогичными рядами описывается поле силы тяжести Земли.

Для удобства решения различных задач Г. и. З. условно разделяется на нормальную и аномальную части. Основная — нормальная часть, описываемая несколькими первыми членами разложения, соответствует идеализированной Земле («нормальной» Земле) простой геометрической формы и с простым распределением плотности внутри неё. Аномальная часть поля меньше по величине, но имеет сложное строение. Она отражает детали фигуры и распределения плотности реальной Земли. Нормальная часть поля силы тяжести рассчитывается по формулам распределения ускорения нормальной силы тяжести g. В СССР и др. социалистических странах наиболее часто используется формула Гельмерта (1901—09):

g = 978030 (1 + 0,005302 sin 2j — —0,000007sin 22j) мгл .

Формула Кассиниса (1930), называемая международной, имеет вид:

g = 978049 (1 + 0,0052884 sin 2j — 0,0000059 sin 22j) мгл .

Существуют другие, менее распространённые, формулы, учитывающие небольшое долготное изменение g, а также асимметрию Северного и Южного полушарий. Ведётся подготовка к переходу к единой новой формуле с учётом уточнённого абсолютного значения силы тяжести. С помощью формул распределения нормальной силы тяжести, зная высоты пунктов наблюдений, а также строение окружающего рельефа и плотности слагающих его пород, вычисляют аномалии силы тяжести , которые применяются для решения большинства задач гравиметрии.

Потенциал силы тяжести используется при изучении фигуры Земли, близкой к уровенной поверхности Г. п. З., а также в астродинамике при изучении движения искусственных спутников в Г. п. З. (уровенной называется поверхность, во всех точках которой потенциал имеет одинаковое значение; сила тяжести направлена к ней по нормали). Одна из уровенных поверхностей, которая совпадает с невозмущённой средней поверхностью океанов, называется геоидом . По направлению силы тяжести устанавливается отвес и определяется положение астрономического зенита. Поскольку уклонения отвеса приближённо равны отношению горизонтальной составляющей притяжения к силе тяжести, то знание их величин в определённом смысле позволяет судить и о Г. п. З.

Вторые производные потенциала силы тяжести применяются при решении геологоразведочных и геодезических задач. Вертикальный градиент силы тяжести , соответствующий нормальной части Г. п. З., от полюса к экватору изменяется всего на 0,1% от его полной величины, равной в среднем для всей Земли 3086 этвеш . Намного меньше по абсолютной величине нормальные горизонтальные градиенты силы тяжести и вторые производные потенциала силы тяжести, характеризующие кривизну уровенной поверхности Земли. Аномальная часть вторых производных потенциала позволяет судить о плотностных неоднородностях в верхних частях земной коры. По величине она достигает в равнинных местах десятков, а в горных — сотен этвеш . В гравиметрической разведке , помимо вторых производных потенциала силы тяжести, используются третьи производные потенциала, получаемые путём пересчёта по аномалиям силы тяжести. Сила тяжести измеряется гравиметрами и маятниковыми приборами , а вторые производные потенциала силы тяжести — гравитационными вариометрами .