БСЭ БСЭ - Большая Советская Энциклопедия (ГР)

Графе'ма(от греч. grapho — пишу), мельчайшая смыслоразличительная единица письменной речи, соответствующая фонеме в устной речи, например «а», «б» и т. д. Система Г. определённой письменности образует алфавит этой письменности. От Г. следует отличать литеру (букву), соответствующую звуку речи (например, А, а, а и т. д.), и графическое сочетание (т. е. совокупность литер), регулярно используемое в данной письменности для обозначения той или иной фонемы (например, ch — «ш» во французском, «х» в нем., «ч» в английском письме). Термин «Г.» введён в 1912 И. А. Бодуэном де Куртенэ .

Лит.: Бодуэн де Куртенэ И. А., Об отношении русского письма к русскому языку, СПБ, 1912; Волоцкая З. М., Молошная Т. Н., Николаева Т. М., Опыт описания русского языка в его письменной форме, М., 1964.

А. Г. Шицгал.

Графена'уэр(Grafenauer) Бого (р. 16.3.1916, Любляна), югославский историк. Окончил философский факультет Люблянского университета, с 1951 профессор этого университета. Специалист по истории Словении. Основные работы посвящены расселению славян на Балканах, истории Великой Карантании, крестьянскому движению 16—18 вв., 1848—49. В 1946 участвовал в международной комиссии по установлению границы Югославии с Италией и Австрией.

Соч.: Boj za sJaro pravdo. Slovenski kmet ob koncu 15 in zacetku 16 stoletja, Ljubljana, 1944; Ustolicavanje Koroskih vojvod in drzava karantinskih slovencev, Ljubljana, 1952; Zgodovina sloyenskega naroda, 2 izd., sv. I—2, Ljubljana, 1964—65.

И. В. Чуркина.

Гра'фик,геометрическое изображение функциональной зависимости при помощи линии на плоскости. Например, на рис. 1 изображен Г. изменения атмосферного давления со временем. Г. применяют как для наглядного изображения функциональных зависимостей и придания наглядности их исследованию, так и для быстрого фактического нахождения значений функций по значениям аргументов. Виды Г. очень разнообразны и зависят от того, какая система координат на плоскости положена в их основу. Если система координат выбрана, то Г. функции f ( x ) есть не что иное, как множество (или, как иначе говорят, «геометрическое место») тех точек плоскости, координаты которых удовлетворяют уравнению y = f ( x ). В большинстве случаев Г. строят в декартовых прямоугольных координатах. На рис. 2 изображен Г. функции у = х 2 — парабола, а на рис. 3 — Г. функции 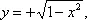представляющий полуокружность, начинающуюся в точке с координатами (—1, 0) и кончающуюся в точке с координатами (+1, 0).

В прямоугольной системе координат масштабы по осям одинаковы; на практике от этого неудобного ограничения отказываются, выбирая разные масштабы по осям координат так, чтобы наилучшим образом использовать площадь листа бумаги, отводимую для Г. Употребляются также Г., основанные на других системах координат, например полярной; последняя особенно удобна для изображения функций углового аргумента (на рис. 4 даны построенные в полярной системе координат Г. распределения силы света, испускаемого по различным направлениям тремя типами дуговых фонарей). Иногда для упрощения вида Г. целесообразно принимать за координаты точки те или иные функции от переменных х и у . (О возникающем отсюда особом способе графического изображения функций см. ст. Номография .) Например , если значениям аргумента и функции — значениям ( х , у ) — ставить в соответствие точку с декартовыми координатами (lg x , lg y ), то Г. функции у = х n при любом показателе n оказываются прямолинейными ( рис. 5 ). Для быстрого вычерчивания подобных Г. служит полулогарифмическая и логарифмическая бумага .

Если Г. является прямой линией или дугой окружности, то его можно строить с помощью линейки или циркуля по двум, соответственно трём точкам. В остальных случаях для вычерчивания Г. приходится наносить на бумагу достаточно большое число принадлежащих ему точек, а затем проводить через эти точки линию Г. «на глаз». Эта операция, всегда несколько произвольная, во всяком случае имеет смысл лишь в предположении непрерывности функции. Если функция не только непрерывная, но и достаточно «гладкая» (т. е. её производные первых двух-трёх порядков меняются с изменением аргумента не слишком быстро), то при некотором навыке проведение Г. по точкам делается очень точно. Нанеся на один чертёж Г. функций y = j 1( x ) и y = j 2( x ), по точкам их пересечения можно определить корни уравнения j 1( x ) = j 2( x ) (см. рис. 3 в ст. Графические вычисления ).

Существует большое число самопишущих приборов, автоматически наносящих на бумагу Г. наблюдаемой функциональной зависимости, минуя её аналитическое выражение (например, барограф , строящий Г. давления атмосферы в функции времени). Часто для графического изображения зависимости между величинами пользуются диаграммами . В экономике и организации производства распространение получили контрольные и плановые Г. ( см . Графические методы в управлении производством) и организационные Г., изображающие организационные связи и зависимости (например, схема управления предприятием). Во многих вопросах целесообразно одновременно рассматривать Г. нескольких различных функций, изображая их на одном и том же чертеже. Типичным примером таких Г. являются графики движения на транспорте.

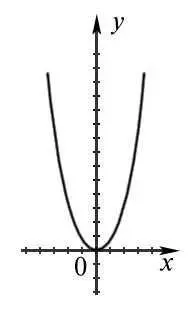
Рис. 2. График функции у = х 2 (парабола).

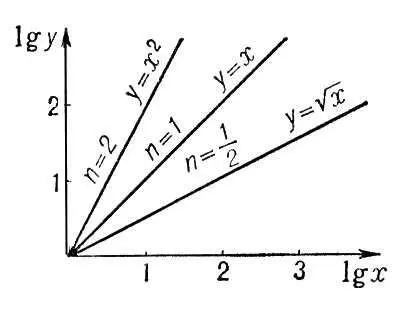
Рис. 5. Графики функции у = x n при n = 1/ 2, 1, 2. По осям координат отложены lg x и lg y .

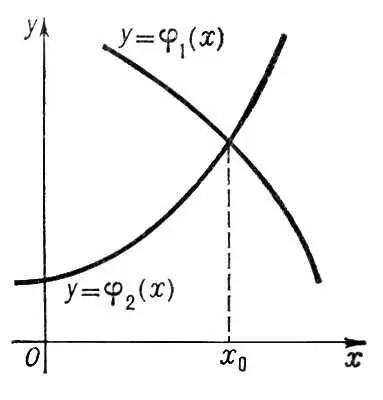
Графическое решение уравнения j 1( x ) = j 2( x ).

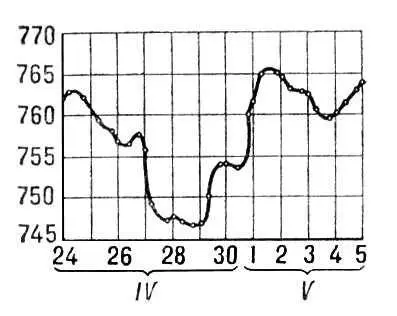
Рис. 1. График изменения атмосферного давления (в мм рт. ст .) за время от 24 апреля до 5 мая.

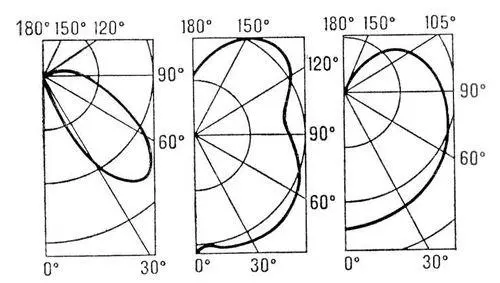
Рис. 4. График в полярных координатах. Диаграмма направленности силы света трёх типов дуговых фонарей.

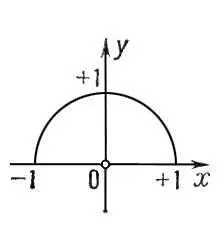
Рис. 3. График функции 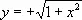(полуокружность).