БСЭ БСЭ - Большая Советская Энциклопедия (ГР)

Комбинируя действия умножения и сложения, графически вычисляют суммы произведений вида

a 1 x 1+ a 2 x 2+ ... + a n x n

и взвешенное среднее

( a 1 x 1+ ... + a n x n)/( a 1+ ... + а 2).

Графическое возведение в целую степень заключается в последовательном повторении умножения.

Построение значений многочлена

f ( x ) = a 0 x n+ a 1 x n-1+ ... + a n-1 x + a n

основано на представлении его в виде

f ( x ) = {[( a 0 x + a 1) х + а 2] х + ...} х + а n

и последовательном графическом выполнении действий, начиная с выражения, заключённого во внутренние скобки.

Графическое решение уравнения f ( x ) = 0 заключается в вычерчивании графика функции у = f ( x ) и нахождении абсцисс точек пересечения кривой с осью Ox , которые и дают значения корней уравнения. Иногда решение можно значительно упростить, если представить уравнение в виде j 1( x ) = j 2( x ) и вычертить кривые y = j 1( x ) и y = j 2( x ). Корнями уравнения будут значения абсцисс точек пересечения этих кривых (на рис. 3 показано нахождение корня x 0).

Так, для решения уравнения третьей степени z 3+ az 2+ bz + c = 0 его приводят к виду x 3+ px + q = 0 заменой z = х — а /3, затем уравнение представляют в виде x 3= — px — q и вычерчивают кривую у = х 3и прямую у =— px — q . Точки их пересечения определяют корни x 1, x 2, x 3уравнения. Построение удобно тем, что кубическая парабола у = х 3 остаётся одной и той же для всех уравнений третьей степени. На рис. 4 решено уравнение x 3— 2,67 x — 1 = 0. Его корни x 1= —1,40, x 2= — 0,40, x 3= 1,80. Аналогично решается уравнение четвёртой степени z 4+ az 3+ bz 2+ cz + d = 0. Подстановкой z = x — a /4 его приводят к виду x 4+ px 3+ qx + s = 0 и затем переходят к системе уравнений: у = х 2, ( х – х 0) 2+ ( у — у 0) 2= r 2, вводя переменное y . Здесь x 0= —q /2, у 0= (1 – р )/2 и 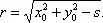Первое уравнение даёт на плоскости параболу, одну и ту же для всех уравнений четвёртой степени, второе — окружность радиуса г , координаты центра x 0, y 0которой легко подсчитать по коэффициенту данного уравнения. На рис. 5 решено уравнение x 4 — 2,6 x 2— 0,8 х — 0,6 = 0 (для него x 0= 0,4; y 0= 1,8, r = 2). Его корни x 1= — 1,55, x 2= 1,80. Как видно из рис. , уравнение др. действительных корней не имеет.

Графическое интегрирование.Вычисление определенного интеграла 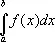основано на замене графика подинтегральной функции y = f ( x ) ступенчатой ломаной. На рис. 6 изображена криволинейная трапеция aABb , площадь которой численно равна вычисляемому интегралу. Для построения ломаной криволинейную трапецию разрезают прямыми, параллельными оси Оу , на ряд полос — элементарных криволинейных трапеций. В каждой из них отрезок кривой заменяют отрезком, параллельным оси Ox , так, чтобы получающиеся прямоугольники имели примерно ту же площадь, что и соответствующие элементарные криволинейные трапеции (ломаная изображена на рис. 6 жирной линией). Площадь, ограниченная ломаной, равна сумме площадей построенных прямоугольников, т. е. 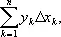D x k— длина основания k- гo прямоугольника, y k — одно из значений функции у = f ( x ) на отрезке D x k, равное высоте прямоугольника. Это выражение принимают за приближённое значение интеграла 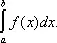Сумму 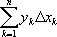вычисляют графически так, как уже было указано. На рис. 7 выполнены все построения, необходимые для вычисления интеграла 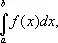где функция y = f ( x ) задана графиком AC 0... C 4 B . После разбиения криволинейной трапеции на части прямыми, проходящими через точки A 1, ..., A 4 , построены прямоугольники. Высоты их, ординаты точек C 0, ..., C 4, снесены на ось Оу . Полученные точки P 0, ..., P 4соединены с точкой Р ( OP = 1). Затем, начиная от точки а , построена ломаная aB 1... B 5, звенья которой параллельны соответствующим отрезкам PP 0, PP 1, ..., PP 4. Величина интеграла численно равна ординате точки B 5. Для построения графика первообразной функции y = f ( x ), т. е. 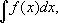достаточно соединить плавной кривой вершины ломаной, получаемой при вычислении 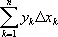(на рис. 7 точки B 0, B 1, ..., B 5).

Графическое дифференцирование. График производной можно строить по значениям тангенса угла наклона касательной к графику данной функции в различных его точках. Точность такого построения мала из-за больших погрешностей при определении направлений касательных. График производной строят также по секущим, повторяя в обратном порядке процесс графического интегрирования, изображенный на рис. 7 . Для этого график функции ( рис. 8 ) разбивают на части прямыми, параллельными оси Оу и проведёнными через равные расстояния D x. Через точки деления A 1, A 2, ... проводят отрезки AB 1, A 2 B 2, …, параллельные оси Ox . Отрезки B 1 A 1 , B 2 A 2, ... равны соответствующим приращениям функции. Их откладывают от оси Ox . По полученным точкам 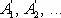строят ступенчатую ломаную. Затем проводят кривую, следя за тем, чтобы криволинейные треугольники в пределах одной ступени ломаной имели равные площади. Эта кривая и является графиком производной.

Графическое интегрирование дифференциальных уравнений.Дифференциальное уравнение первого порядка dy / dx = f ( x , у ) определяет на плоскости поле направлений. Задача интегрирования уравнения заключается в проведении кривых, касательные к которым имеют направления поля. Различные приёмы графического интегрирования состоят в последовательном построении интегральных кривых по касательным, направления которых заданы, и в известной мере повторяют численные методы интегрирования (см. Приближённое решение дифференциальных уравнений).