БСЭ БСЭ - Большая Советская Энциклопедия (ДО)

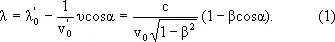
В формуле (1) l — длина принимаемой волны, l¢ 0— длина испускаемой волны, b= v/c . Множитель

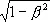
учитывает замедление времени в системе движущегося источника, в результате которого измеренное значение частоты n' 0одного и того же колебания в системе наблюдателя оказывается ниже, чем в системе источника n 0(в этом сказывается различие течения времени в системах движущегося источника и наблюдателя — эффект специальной теории относительности).

Уравнение (1) позволяет найти частоту колебаний, воспринимаемых наблюдателем,

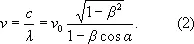
При движении источника к наблюдателю (a = 0, cos a = 1) или от наблюдателя (a = p, cos a = -1) имеет место продольный Д. э.:

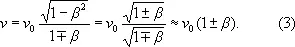
При сближении источника и наблюдателя частота n принимаемых колебаний возрастает, при удалении — убывает. Продольный Д. э. даёт максимально возможное изменение частоты при данной скорости.

Если источник движется вокруг наблюдателя по окружности [в формуле (2) a = ± p/ 2, cos a = 0], то и в этом случае воспринимаемая частота отличается от излучаемой

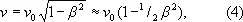
хотя число длин волн, укладывающихся на пути распространения, остаётся неизменным. Формула (4) определяет поперечный Д. э., обусловленный разным ходом времени в системах источника и наблюдателя. Поперечный Д. э. является эффектом второго порядка малости относительно v/c и наблюдать его значительно труднее, чем продольный. В случае сравнения частот в одной системе отсчёта, как, например, при радиолокации, поперечный Д. э. отсутствует.

В тех случаях, когда показатель преломления n среды, в которой движется источник, отличается от 1 и зависит от частоты, значение воспринимаемой частоты соответствует решению уравнения

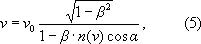
где n (n) — показатель преломления, зависящий от частоты n. В области частот, где эта зависимость выражена очень резко (см. Дисперсия волн ), уравнение (5) может иметь несколько решений (сложный Д. э.).

В среде с изменяющимся во времени показателем преломления Д. э. возникает и при неподвижных друг относительно друга источнике и приёмнике. Подобное явление может иметь место при космической связи, когда радиолуч проходит через ионосферу Земли с переменным показателем преломления.

Понятие Д. э. обобщается и на изменение частоты электромагнитного излучения в гравитационном поле (эффект теории тяготения Эйнштейна). Например, некоторая линия солнечного спектра с частотой n 0будет наблюдаться на Земле как линия с частотой

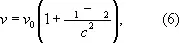
где j 1и j 2— гравитационные потенциалы Солнца и Земли (j 1и j 2< 0). При наблюдении на Земле излучения Солнца и звёзд линии смещаются под действием гравитации в область более низких частот, т.к. |j 1| > |j 2|.

Д. э. назван в честь австрийского физика К. Доплера , обосновавшего теоретически (1842) этот эффект в акустике и оптике. Русский физик В. А. Михельсон распространил его на случай среды с переменными параметрами (1899). Существование поперечного Д. э. было экспериментально подтверждено американскими физиками Г. Айвсом и Д. Стилуэллом (1938).

С момента открытия Д. э. используется для определения лучевых скоростей звёзд и вращения небесных тел. Изучение доплеровского смещения линий в спектрах удалённых галактик привело к представлению о расширении Метагалактики (см. Красное смещение , Космология ). По доплеровскому уширению спектральных линий в оптическом и радиодиапазонах методами спектроскопии определяются тепловые скорости атомов и ионов в звёздных атмосферах и межзвёздном газе, изучается структура внегалактических радиоисточников. В радиолокации и гидролокации Д. э. служит для определения скорости движения цели. Д. э. используется также в космической навигации. В радиолокационной астрономии с помощью Д. э. разделяют отражения от участков поверхности небесного тела с различными лучевыми скоростями.

Лит.: Ландау Л. Д., Лифшиц Е. М., Теория поля, М., 1967 (Теоретическая физика, т. 2); Ландсберг Г. С., Оптика, 4 изд., М., 1957 (Общий курс физики, т. 3); Франк И. М., Эффект Доплера в преломляющей среде, «Изв. АН СССР. Серия физическая», 1942, №1—2; Сколник М., Введение в технику радиолокационных систем, пер. с англ., М., 1965.

О. Н. Ржига.

Дополне'ние,второстепенный член предложения, которым выражается объект действия, поясняется сказуемое, а также и др. члены предложения («я читаю книгу», «я начертил план карандашом»). Д. бывают приглагольные («люблю молоко», «люблю читать») и приименные («полный надежд», «стакан воды»).

«Дополне'ния к а'ктам истори'ческим»[«Дополнения к актам историческим, собранные и изданные Археографической комиссией» («ДАИ»), т. 1—12, СПБ, 1846—75]. В издание вошло 1800 ценных документов по истории России 12—17 вв., извлечённых из центральных и многочисленных местных архивов, а также частных собраний. Ряд документов, хранящихся в Стокгольмском архиве, напечатан по копиям. В «ДАИ» опубликованы уникальные документы — так называемые церковные уставы князя Владимира и жалованная грамота великого князя Всеволода Мстиславича церкви Иоанна Предтечи на Опоках и др., а также духовное завещание Ивана IV 1572, акты о Строгановых, о тульских и каширских железных заводах и др. документы по истории колонизации Сибири и о великих географических открытиях, о Псковском восстании 1650, крестьянской войне под предводительством С. Т. Разина , Соловецком восстании 1668—76 (послания киевского митрополита Фотия, Иосифа Волоцкого, московского митрополита Макария и др.). К первым 10 тт. «ДАИ» имеется именной и географический указатель (СПБ, 1875).

В. И. Корецкий.

Дополни'тельная опла'та труда' колхо'зников,см. Оплата труда в колхозах .

Дополни'тельности при'нцип,сформулированное Н. Бором положение, сыгравшее важную роль в становлении квантовой механики , согласно которому получение экспериментальных данных об одних физических величинах, описывающих микрообъект (например, электрон, протон, атом), неизбежно связано с изменением таких данных о величинах, дополнительных к первым. Такими взаимно дополнительными величинами являются, например, координата и импульс частицы. Д. п. содержится в принципе неопределённостей, математическим выражением которого являются неопределённостей соотношения .