БСЭ БСЭ - Большая Советская Энциклопедия (ЗН)

Начатки буквенного изображения и исчисления возникают в позднеэллинистическую эпоху в результате освобождения алгебры от геометрической формы. Диофант (вероятно, 3 в.) записывал неизвестную ( х ) и её степени следующими знаками:

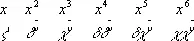
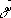[ — от греческого термина dunamiV (dynamis — сила), обозначавшего квадрат неизвестной, 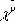— от греческого cuboV (k_ybos) — куб]. Справа от неизвестной или её степеней Диофант писал коэффициенты, например 3х 5изображалось

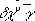
(где 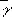= 3). При сложении Диофант приписывал слагаемые друг к другу, для вычитания употреблял специальный знак 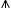; равенство Диофант обозначал буквой i [от греческого isoV (isos) — равный]. Например, уравнение

( x 3+ 8 x ) — (5 x 2+ 1) = х

у Диофанта записалось бы так:

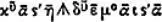
(здесь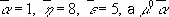

означает, что единица 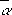не имеет множителя в виде степени неизвестного).

Несколько веков спустя индийцы ввели различные З. м. для нескольких неизвестных (сокращения наименований цветов, обозначавших неизвестные), квадрата, квадратного корня, вычитаемого числа. Так, уравнение

3 х 2+ 10 x — 8 = x 2+ 1

в записи Брахмагупты (7 в.) имело бы вид:

йа ва 3 йа 10 ру 8

йа ва 1 йа 0 ру 1

(йа — от йават — тават — неизвестное, ва — от варга — квадратное число, ру — от рупа — монета рупия — свободный член, точка над числом означает вычитаемое число).

Создание современной алгебраической символики относится к 14—17 вв.; оно определялось успехами практической арифметики и учения об уравнениях. В различных странах стихийно появляются З. м. для некоторых действий и для степеней неизвестной величины. Проходят многие десятилетия и даже века, прежде чем вырабатывается тот или иной удобный символ. Так, в конце 15 и. Н. Шюке и Л. Пачоли употребляли знаки сложения и вычитания

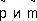
(от лат. plus и minus), немецкие математики ввели современные + (вероятно, сокращение лат. et) и —. Ещё в 17 в. можно насчитать около десятка З. м. для действия умножения.

Различны были и З. м. неизвестной и её степеней. В 16 — начале 17 вв. конкурировало более десяти обозначений для одного только квадрата неизвестной, например се (от census — латинский термин, служивший переводом греческого dunamiV, Q (от quadratum), , A (2), 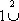, Aii, aa , a 2 и др. Так, уравнение

x 3+ 5 x = 12

имело бы у итальянского математика Дж. Кардано (1545) вид:

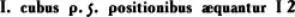
у немецкого математика М. Штифеля (1544):

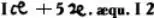
у итальянского математика Р. Бомбелли (1572):

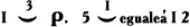
французского математика Ф. Виета (1591):

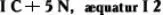
у английского математика Т. Гарриота (1631):

В 16 и начале 17 вв. входят в употребление знаки равенства и скобки: квадратные (Р. Бомбелли , 1550), круглые (Н. Тарталья, 1556), фигурные (Ф. Виет, 1593). В 16 в. современный вид принимает запись дробей.

Значительным шагом вперёд в развитии математической символики явилось введение Виетом (1591) З. м. для произвольных постоянных величин в виде прописных согласных букв латинского алфавита В, D, что дало ему возможность впервые записывать алгебраические уравнения с произвольными коэффициентами и оперировать ими. Неизвестные Виет изображал гласными прописными буквами А, Е,... Например, запись Виета

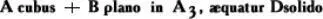
[cubus — куб, planus — плоский, т. е. В — двумерная величина; solidus — телесный (трёхмерный), размерность отмечалась для того, чтобы все члены были однородны] в наших символах выглядит так:

x 3 + 3 bx = d.

Виет явился творцом алгебраических формул. Р. Декарт (1637) придал знакам алгебры современный вид, обозначая неизвестные последними буквами лат. алфавита х, у, z, а произвольные данные величины — начальными буквами а, b, с. Ему же принадлежит нынешняя запись степени. Обозначения Декарта обладали большим преимуществом по сравнению со всеми предыдущими. Поэтому они скоро получили всеобщее признание.

Дальнейшее развитие З. м. было тесно связано с созданием анализа бесконечно малых, для разработки символики которого основа была уже в большой мере подготовлена в алгебре.

Даты возникновения некоторых математических знаков

знак	значение	Кто ввёл	Когда введён
Знаки индивидуальных объектов
¥	бесконечность	Дж. Валлис	1655
e'	основание натуральных логарифмов	Л. Эйлер	1736
p	отношение длины окружности к диаметру	У. Джонс Л. Эйлер	1706 1736
i	корень квадратный из -1	Л. Эйлер	1777 (в печати 1794)
i j k	единичные векторы, орты	У. Гамильтон	1853
П (а)	угол параллельности	Н.И. Лобачевский	1835
Знаки переменных объектов
x,y, z'	неизвестные или переменные величины	Р. Декарт	1637
r	вектор	О. Коши	1853
Знаки индивидуальных операций
+	сложение	немецкие математики	Конец 15 в.
–'	вычитание
´	умножение	У. Оутред	1631
×	умножение	Г. Лейбниц	1698
:	деление	Г. Лейбниц	1684
a 2, a 3,…, a n	степени	Р. Декарт	1637
	И. Ньютон	1676
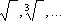	корни	К. Рудольф	1525
А. Жирар	1629
Log	логарифм	И. Кеплер	1624
log	Б. Кавальери	1632
sin	синус	Л. Эйлер	1748
cos	косинус
tg	тангенс	Л. Эйлер	1753
arc.sin	арксинус	Ж. Лагранж	1772
Sh	гиперболический синус	В. Риккати	1757
Ch	гиперболический косинус
dx, ddx, …	дифференциал	Г. Лейбниц	1675 (в печати 1684)
d 2x, d 3x,…
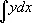	интеграл	Г. Лейбниц	1675 (в печати 1686)
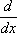	производная	Г. Лейбниц	1675
¦¢x	производная	Ж. Лагранж	1770, 1779
y’
¦¢(x)
Dx	разность	Л. Эйлер	1755
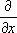	частная производная	А. Лежандр	1786
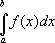	определённый интеграл	Ж. Фурье	1819-22
S	сумма	Л. Эйлер	1755
П	произведение	К. Гаусс	1812
!	факториал	К. Крамп	1808
|x|	модуль	К. Вейерштрасс	1841
lim	предел	У. Гамильтон, многие математики	1853, начало 20 в.
lim
n = ¥
lim
n ® ¥
x	дзета-функция	Б. Риман	1857
Г	гамма-функция	А. Лежандр	1808
В	бета-функция	Ж. Бине	1839
D	дельта (оператор Лапласа)	Р. Мёрфи	1833
Ñ	набла (оператор Гамильтона)	У. Гамильтон	1853
Знаки переменных операций
jx	функция	И. Бернули	1718
f ('x)	Л. Эйлер	1734
Знаки индивидуальных отношений
='	равенство	Р. Рекорд	1557
>'	больше	Т. Гарриот	1631
<'	меньше
º	сравнимость	К. Гаусс	1801
||	параллельность	У. Оутред	1677
^	перпендикулярность	П. Эригон	1634

И. Ньютон в своём методе флюксий и флюент (1666 и следующие гг.) ввёл знаки для последовательных флюксий (производных) величины (в виде