БСЭ БСЭ - Большая Советская Энциклопедия (ИС)

Соч.: Сайланма эсэрлэр, Казан, 1965; в рус. пер. — Стихи, Каз., 1956; Встреча в песне, М., 1960.

Лит.: Хэким С., «Курай», «Совет эдэбияты», 1946, № 11—12.

Исхо'д,вторая книга Пятикнижия .

Исхо'дные геодези'ческие да'ты,совокупность величин, определяющих положение референц-эллипсоида , принятого для обработки геодезической сети какой-либо страны или группы стран, относительно геоида , т. е. величин, фиксирующих положение референц-эллипсоида в теле Земли. В состав И. г. д. входят геодезические координаты (см. Координаты в геодезии), а именно широта B 0и долгота L 0одного из опорных пунктов сети, принятого за исходный, геодезический азимут A 0направления с исходного пункта на один из смежных пунктов сети и высота x 0исходного пункта над геоидом. И. г. д. устанавливаются после вывода референц-эллипсоида путём определения астрономических координат (j 0, l 0) (см. Географические координаты ) исходного пункта и астрономического азимута a указанного выше направления и освобождения их от влияния уклонений отвеса. Геодезические координаты всех остальных пунктов сети и азимуты получают затем путём вычислений на основании результатов геодезических измерений, приведённых к поверхности референц-эллипсоида. Геодезические координаты пунктов астрономо-геодезической сети СССР и некоторых других стран вычисляются на поверхности Красовского эллипсоида . Исходным пунктом геодезической сети СССР служит центр бывшего Круглого зала Пулковской астрономической обсерватории, для которого приняты следующие геодезические координаты: широта B 0= 59°46¢18¢¢, 55, долгота L 0= 30°19¢42¢¢,09, высота x 0положена равной нулю. Вывод указанных И. г. д. СССР выполнили А. А. Изотов и М. С. Молоденский в 1942. Эти И. г. д., как и эллипсоид Красовского, приняты за основу единой государственной системы координат при производстве всех геодезических и картографических работ на территории СССР.

С начала 60-х гг. 20 в. методы космической геодезии позволили на основе наблюдений искусственных спутников Земли получать параметры земного эллипсоида , представляющего Землю в целом, и развивать единую мировую геодезическую систему координат, связывающую воедино разрозненные астрономо-геодезические сети отдельных материков и стран. Это имеет большое научное и практическое значение для решения проблем геодезии и ряда смежных наук. Несвязанные до этого астрономо-геодезические сети, обработанные ранее при различных И. г. д. и на разных референц-эллипсоидах, могут быть теперь отнесены к единой мировой геодезической системе координат на одном эллипсоиде, наиболее подходящем к Земле как планете в целом, или к единой мировой системе прямоугольных декартовых координат.

Лит.: Закатов П. С., Курс высшей геодезии, М., 1964; Изотов А. А., Новые исходные геодезические даты СССР, в кн.: Сборник научно-технических и производственных статей по геодезии, картографии, топографии, аэросъёмке и гравиметрии, в. 17, М., 1948; Стандартная Земля. Геодезические параметры Земли на 1966 год. [Сб. ст.], пер. с англ., М., 1969.

Г. А. Мещеряков.

Исче'рпывания ме'тод,метод доказательства, применявшийся математиками древности при нахождении площадей и объёмов. Название «метод исчерпывания» введено в 17 в.

Типичная схема доказательства при помощи И. м. может быть изложена в современных обозначениях так: для определения величины А строится некоторая последовательность величин C 1, C 2, ..., C n, ... так, что

C n < A ; (1)

предполагают также известным такое В , что

C n < В (2)

и при любом целом К для достаточно больших n удовлетворяются неравенства

К ( A — C n ) < D , К ( В — C n ) < D , (3)

где D — постоянно. С современной точки зрения, для перехода от неравенств (3) к равенству

А = В (4)

достаточно заметить, что из условий (1), (2) и (3) следует

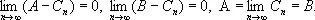
Математики древности, не располагавшие теорией пределов , обращались к доказательству от противного и доказывали невозможность каждого из неравенств А < В , В < А . Чтобы опровергнуть первое из них, при помощи аксиомы Евдокса — Архимеда (см. Архимеда аксиома ) устанавливали, что для R = B — А существует такое К , что KR > D и в силу условия (1) получали

К ( В — C n ) > К ( В — A ) > D ,

что противоречит второму из неравенств (3). Аналогично опровергалось другое предположение. После этого оставалось принять только равенство (4).

Введение И. м. вместе с лежащей в его основе аксиомой приписывается Евдоксу Книдскому. Этим методом широко пользовался Евклид, а с особенным искусством и разнообразием — Архимед. Например, для определения площади сегмента А параболы Архимед строит площади C 1, C 2, ..., «исчерпывающие» при их постепенном нарастании площадь A сегмента, по схеме, ясной из чертежа. При этом

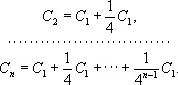
Вместо того чтобы прибегнуть к предельному переходу,

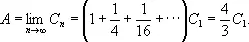
Архимед геометрически доказывает, что при любом n

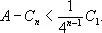
Вводя площадь

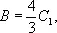
Архимед получает, что

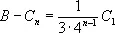
и, следуя изложенному выше порядку, заканчивает доказательство того, что

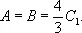
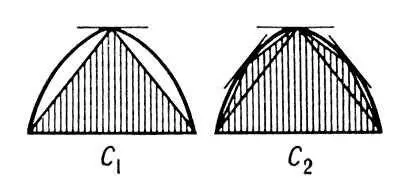
Рис. к ст. Исчерпывания метод.

Исчисле'ние,основанный на чётко сформулированных правилах формальный аппарат оперирования со знаками определённого вида, позволяющий дать исчерпывающе точное описание некоторого класса задач, а для некоторых подклассов этого класса (лишь для наиболее простых И., совпадающих с ним) — и алгоритмы решения. Примерами И. могут служить совокупность арифметических правил оперирования с цифрами (т. е. числовыми знаками), «буквенное» И. элементарной алгебры, дифференциальное И., интегральное И., вариационное И. и другие ветви математического анализа и теории функций. Несмотря на раннее происхождение, термин «И.» употреблялся в математике до недавнего времени без строгого общего определения. С развитием математической логики возникла потребность в общей теории И. и в уточнении самого понятия «И.», которое подверглось более последовательной формализации. В большинстве случаев, однако, оказывается достаточным следующее (идущее от Д. Гильберта ) представление об И. Рассматривается некоторый (вообще говоря, бесконечный, хотя и, быть может, задаваемый посредством конечного числа символов) алфавит, из элементов которого, именуемых буквами, с помощью четко сформулированных правил образования строятся формулы рассматриваемого И. (называемые также иногда словами, или выражениями). Некоторые из таких («правильно построенных») формул объявляются аксиомами, а из них с помощью правил преобразования (или, иначе, правил вывода) «выводятся» новые формулы, называемые теоремами данного И. Иногда термин «И.» относят лишь к «словарной» («выразительной») части описанного построения, говоря, что присоединение к ней «дедуктивной» части (т. е. добавление к алфавиту и правилам образования аксиом и правил ввода) даёт формальную систему. Впрочем, эти термины часто считают синонимичными (и в качестве синонимов пользуются также терминами «логистическая система», «формализм», «формальная теория» и многими др.). Если такое неинтерпретированное («бессмысленное») И. сопоставить с некоторой интерпретацией (или, как говорят, дополнить чисто синтаксические рассмотрения некоторой семантикой; см. Логическая семантика ) то получают формализованный язык . Представление содержательных логических (и логико-математических) теорий в виде формализованных языков есть характерная особенность математической логики (см. также Доказательство ).