БСЭ БСЭ - Большая Советская Энциклопедия (КЛ)

Г. Г. Мирзабеков

Клапаре'д(Claparede) Эдуар (24.3.1873, Женева, — 29.9.1940, там же), швейцарский психолог. Профессор Женевского университета (с 1908), один из основателей Педагогического института им. Ж. Ж. Руссо в Женеве (1912), ставшего международным центром экспериментальных исследований в области детской психологии. В 1920 основал «Международное общество психотехники». В противоположность ассоцианизму в психологии К., примыкая к В. Вундту, Т. Рибо и У. Джемсу, развивал учение об активности сознания. К. — представитель «функциональной психологии» — биологической науки, рассматривающей психические явления с точки зрения их функции в жизненном процессе, их места «в ансамбле поведения». В этом плане понятие интереса — центральное в концепции К. Психические функции, в том числе интеллект и воля, развиваются, по К., для удовлетворения тех или иных потребностей организма, причем сознательные акты проявляются тогда, когда на пути рефлекторных актов встречается какое-либо препятствие. К. выдвинул идею о качественно различных уровнях в онтогенезе процесса обобщения, которая оказала значительное влияние на генетическую психологию, в частности на Ж. Пиаже. Известность получила также теория игры К.

Соч.: L'association des idées, P., 1903; L'éducation fonctionelle. P., 1931; Psychologie de l'enfant et pédagogic expérimentale, t. 1 — Le développement mental, P., 1946; в рус. пер.— Психология ребенка и экспериментальная педагогика, СПБ, 1911; Профессиональная ориентация, ее проблемы и методы, М., 1925; Как определять умственные способности школьников, Л., 1927.

Лит.: Edouard Claparede, Gen., 1941.

М. С. Роговин.

Клапейро'н(Clapeyron) Бенуа Поль Эмиль (26.1.1799, Париж, — 28.1.1864, там же), французский физик, член Парижской АН (1858). Окончил Политехническую школу в Париже (1818). В 1820—30 работал в Петербурге в институте инженеров путей сообщения. По возвращении во Францию был профессором Школы мостов и дорог в Париже. В 1834 обратил внимание на работу С. Карно, повторил его рассуждения и, впервые применив графический метод в термодинамике, придал его результатам геометрическую форму. Исследуя цикл Карно, вывел уравнение состояния идеального газа ( см. Клапейрона уравнение ) . Ввёл зависимость точки плавления и кипения от давления (см. Клапейрона — Клаузиуса уравнение ) .

Соч.: Mémoire sur la puissance motrice de la chaleur, «Journal de l'école royale polytechnique», 1834, t. 14, cah. 23: Mémoire sur la reglement des tiroirs dans les machines a vapeur, «Comptes rendus hebdomadaires des séances de l'Académie des sciences», 1842, t. 14, № 18, p. 632—63; Calcul d'une poutre élastique reposant librement sur des appuis inégalement espacés, там же, 1857, t. 45, № 26.

Лит.: Дубровский О. В., Клапейрон и его работа «О движущей силе теплоты», «Труды Ленинградского кораблестроительного института», 1953, в. 11; Искольдский И. И., Бенуа Клапейрон, «Успехи химии». 1945, т. 14, в. 4.

Клапейро'на — Кла'узиуса уравне'ние,термодинамическое уравнение, относящееся к процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.). Согласно К. — К. у., теплота фазового перехода (например, теплота испарения, теплота плавления) при равновесно протекающем процессе определяется выражением

, (1)

где Т — температура перехода (процесс изотермический), dp/dT — значение производной от давления по температуре при данной температуре перехода, ( V 2—V 1 ) — изменение объёма вещества при переходе его из первой фазы во вторую.

Первоначально уравнение было получено в 1834 Б. П. Э. Клапейроном из анализа Карно цикла для конденсирующегося пара, находящегося в тепловом равновесии с жидкостью. В 1850 P. Клаузиус усовершенствовал уравнение и распространил его на др. фазовые переходы. К. — К. у. применимо к любым фазовым переходам, сопровождающимся поглощением или выделением теплоты (т. н. фазовым переходом 1 рода), и является прямым следствием условий фазового равновесия, из которых оно и выводится.

К. — К. у. может служить для расчёта любой из величин, входящих в уравнение, если остальные известны. В частности, с его помощью рассчитывают теплоты испарения, экспериментальное определение которых сопряжено со значительными трудностями.

Часто К. — К. у. записывают относительно производных dp/dT или dT/dp:

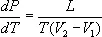(2)

Для процессов испарения и сублимации dp/dT выражает изменение давления насыщенного пара р с температурой Т, а для процессов плавления и полиморфного превращения dT/dp определяет изменение температуры перехода с давлением. Иными словами, К. — К. у. является дифференциальным уравнением кривой фазового равновесия в переменных р, Т.

Для решения К. — К. у. необходимо знать, как изменяются с температурой и давлением величины L, V 1 и V 2, что представляет сложную задачу. Обычно эту зависимость устанавливают эмпирически и решают К. — К. у. численно.

К. — К. у. применимо как к чистым веществам, так и к растворам и отдельным компонентам растворов. В последнем случае К. — К. у. связывает парциальное давление насыщенного пара данного компонента с его парциальной теплотой испарения.

Лит.: Курс физической химии, под ред. Я. И. Герасимова, 2 изд., т. 1, М., 1969.

Ю. И. Поляков.

Клапейро'на уравне'ние,Клапейрона — Менделеева уравнение, найденная Б. П. Э. Клапейроном (1834) зависимость между физическими величинами, определяющими состояние идеального газа: давлением газа р, его объёмом V и абсолютной температурой Т.

К. у. записывается в виде pV = ВТ, где коэффициент пропорциональности В зависит от массы газа. Д. И. Менделеев, используя Авогадро закон, вывел в 1874 уравнение состояния для 1 моля идеального газа pV = RT, где R — универсальная газовая постоянная. Для газа, имеющего общую массу М и молекулярную массу m,

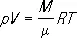, или pV=NkT,'

где N — число частиц газа, k — Больцмана постоянная. К. у. представляет собой уравнение состояния, идеального газа, которое объединяет Бойля — Мариотта закон (зависимость между р и V при Т = const), Гей-Люссака закон (зависимость V от Т при р = const) и Авогадро закон (согласно этому закону, газы при одинаковых значениях р, V и Т содержат одинаковое число молекул N ) .