БСЭ БСЭ - Большая Советская Энциклопедия (КО)

Д. Л. Юдин.

Координато'граф(от координаты и ...граф ) , прибор для быстрого и точного нанесения на карту или план точек по их прямоугольным координатам. Состоит из станины, на которой наглухо прикреплена линейка с делениями, представляющая собой ось абсцисс XX . Вдоль оси абсцисс передвигается каретка, несущая на себе линейку YY, соответствующую оси ординат. По оси ординат движется малая каретка, на которой укреплена иголка для накола точек. Автоматический электронный К. имеет дополнительно счётно-решающее устройство и пульт управления. Эта система обеспечивает возможность по результатам вычислении прямоугольных координат на счётно-решающем устройстве наносить узловые точки и автоматически вычерчивать или гравировать координатные линии сетки.

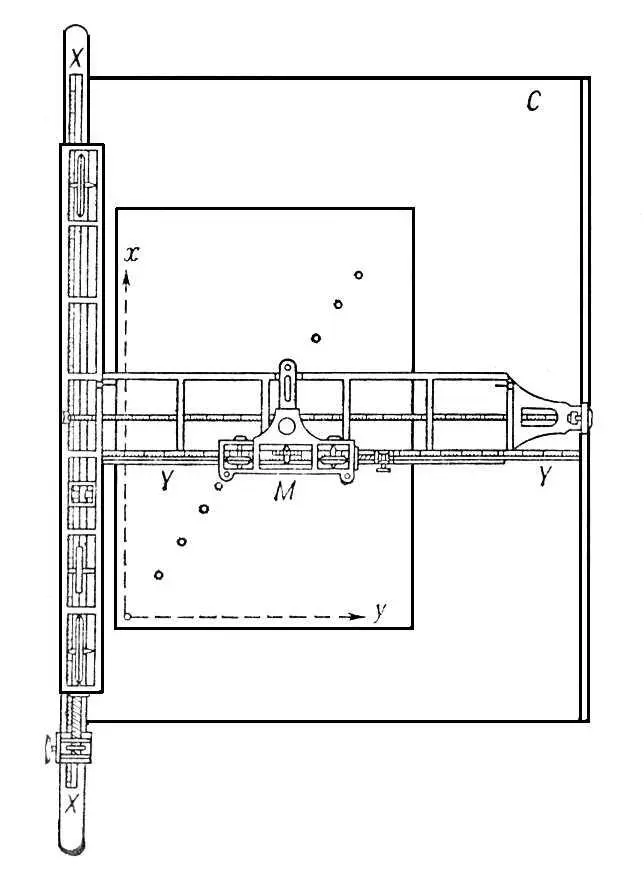
Схема координатографа.

Координатоме'р,прибор для измерения координат точек (ориентиров, целей и т. п.) на топографических картах с прямоугольной координатной сеткой. К. применяют также для нанесения на карты точек по координатам. Иногда К. представляет собой прозрачную прямоугольную плёнку (целлулоидную или др.) с квадратным вырезом посередине и нанесёнными по краям шкалами, равными по длине сторонам квадратов координатной сетки на картах масштабов 1:25000, 1:50000 и 1:100000.

Координа'тыв геодезии, совокупность трёх чисел, определяющих положение точки земной поверхности относительно некоторой исходной поверхности. Последняя, так называемая поверхность относимости, суть поверхность, заменяющая в некотором приближении поверхность геоида. В зависимости от целей за поверхность относимости принимают плоскость (в топографии это плоскость проекции Гаусса—Крюгера, см. Геодезические проекции, Прямоугольные координаты ) , сферу — поверхность «земного шара», поверхность референц-эллипсоида (см. также Земной эллипсоид ) .

Геодезические К. точки: широта В (угол, образованный проходящей через данную точку нормалью эллипсоида с плоскостью его экватора), долгота L (угол между плоскостями меридиана данной точки и начального меридиана), высота Н (расстояние данной точки от эллипсоида по нормали к нему). Геодезические К. непосредственно из наблюдений получены быть не могут. Для любой точки, включенной в геодезическую сеть, они могут быть вычислены по данным геодезических измерений.

Астрономические К. точки: широта j — угол, образованный отвесной линией в данной точке с плоскостью земного экватора; долгота l — угол между плоскостями астрономических меридианов данной точки и начального; так, определённые астрономические координаты j и l называются также географическими координатами. К j и l присоединяется ещё нормальная высота Н g (расстояние данной точки от квазигеоида по отвесной линии), которая часто отождествляется с высотой точки над уровнем моря. Астрономические координаты j и l получают из астрономических наблюдений (см. Геодезическая астрономия ); высоты точек земной поверхности получают из нивелирования. Геодезические К. какой-либо точки отличаются от астрономических К. той же точки за счёт выбора эллипсоида и несовпадения отвесной линии с нормалью к эллипсоиду (см. Отклонение отвеса ) . Сравнение геодезических и астрономических К. ряда точек земной поверхности даёт возможность изучить на данном участке поверхность геоида (точнее квазигеоида) относительно применяемого эллипсоида (астрономическое нивелирование и астрономо-гравиметрическое нивелирование ) .

В геодезии используют также и др. виды К. В связи с развитием космической геодезии большое значение приобрели прямоугольные геодезические координаты X, Y, Z, начало которых О совмещено с центром эллипсоида, а ось Z направлена по малой его оси. Переход от В, L, Н к X, Y, Z совершается по довольно простым формулам.

При изучении многих вопросов геодезии используются также различные криволинейные К. на поверхности эллипсоида. На практике — при использовании данных геодезии и топографических карт — применяют прямоугольные К. на плоскости геодезической проекции.

Лит.: Красовский Ф. Н., Руководство по высшей геодезии, ч. 2, М., 1942; 3акатов П. С., Курс высшей геодезии, 3 изд., М., 1964; Морозов В. П., Курс сфероидической геодезии, М., 1969; Грушинский Н. П., Теория фигуры Земли, М., 1963.

Г. А. Мещеряков.

Координа'ты[от лат. co (cum) — совместно и ordinatus — упорядоченный, определённый], числа, заданием которых определяется положение точки на плоскости, на любой поверхности или в пространстве. Первыми вошедшими в систематическое употребление К. являются астрономические и географические К. — широта и долгота, определяющие положение точки на небесной сфере или на поверхности земного шара (см. Небесные координаты, Географические координаты ) . В 14 в. французский математик Н. Орем пользовался К. на плоскости для построения графиков, называя долготой и широтой то, что теперь называют абсциссой и ординатой. Более систематически К. стали применяться к вопросам геометрии на плоскости в 17 в. Заслуга выяснения всего значения метода К., позволяющего систематически переводить задачи геометрии на язык математического анализа и, обратно, истолковывать геометрически факты анализа, принадлежит французскому учёному Р. Декарту. Кроме К. точки, рассматривают также К. прямой, плоскости и других геометрических объектов. В теоретической механике употребляют К. механических систем — числа, определяющие положение механической системы (например, некоторого твёрдого тела) в каждый момент времени.

Координаты точки на плоскости. Аффинные, или общие декартовы, К. точки на плоскости получают, выбирая точку О (начало К.) и два не лежащих на одной прямой вектора 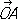и 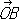, исходящих из точки О . Положение точки Р определяется (в выбранной системе К.) двумя К.: абсциссой

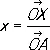
и ординатой

,

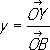где XP параллельно OB и YP параллельно ОА. В частном случае, когда векторы 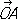и 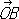перпендикулярны и имеют одну и ту же длину, получают наиболее употребительные прямоугольные К. Если угол между 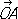и 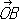произволен, но длины этих векторов одинаковы, то получают те косоугольные К., рассмотрением которых ограничивался сам Декарт (часто только их и называют декартовыми, сохраняя для общих декартовых К. название аффинные К.).