БСЭ БСЭ - Большая Советская Энциклопедия (КВ)

Ква'нтор(от лат. quantum — сколько), логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате её применения. В обычном языке носителями таких характеристик служат слова типа «все», «каждый», «некоторый», «существует», «имеется», «любой», «всякий», «единственный», «несколько», «бесконечно много», «конечное число», а также все количественные числительные. В формализованных языках , составной частью которых является исчисление предикатов , для выражения всех подобных характеристик оказывается достаточным К. двух видов: К. (все) общности (оборот «для всех х », обозначается через "x, ( "x), (x) ( A x), 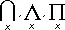) и К. существования («для некоторых х », обозначения: $x, ( $x), (Ех),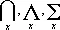

С помощью К. можно записать четыре основных формы суждений традиционной логики: «все А суть В » записывается в виде "x [ A ( x )É É B ( x )], «ни одно A не есть B » — в виде "x [ A ( x )É B ( x )], «некоторые А суть B » — в виде $x [ A ( x )& B ( x )], «некоторые А не суть В » — в виде $x [ A ( x )& B ( x )] (здесь А ( х ) означает, что х обладает свойством A , É — знак импликации , — отрицания , & — конъюнкции ).

Часть формулы, на которую распространяется действие каких-либо К., называется областью действия этого К. (её можно указать с помощью скобок). Вхождение какой-либо переменной в формулу непосредственно после знака К. или в область действия К., после которого стоит эта переменная, называется её связанным вхождением. Все остальные вхождения переменных называются свободными. Формула, содержащая свободные вхождения переменных, зависит от них (является их функцией ); связанные же вхождения переменных можно «переименовывать»; например, записи $ x ( x = 2 y ) и $ z ( z = 2 y ) означают одно и то же, чего нельзя сказать о $ x ( x = 2 y ) и $ x ( x = 2 t ). Применение К. уменьшает число свободных переменных в логическом выражении и превращает (если К. не «фиктивный», т. е. относится к переменной, действительно входящей в формулу) трёхместный предикат в двухместный, двухместный — в одноместный, одноместный — в высказывание. Употребление К. кодифицируется специальными «постулатами квантификации» (присоединение которых к исчислению высказываний по существу и означает расширение его до исчисления предикатов), например, следующими «постулатами Бернайса»: аксиомами A ( t ) É $ xA ( x ) и " xA ( x ) É A ( t ) и правилами вывода «если доказано С É А ( х ) É С , то можно считать доказанным и С É " хA ( х )» и «если доказано А ( х ) É С , то можно считать доказанным и $ хA ( x ) É C » (здесь х не входит свободно в С ).

К К. общности и существования сводятся и др. виды К., например вместо так называемого К. единственности $! x («существует единственный х такой, что») можно писать «обычные» К., заменяя $! xA ( x ) на

$ xA ( x ) & " y " z [ A ( y )& A ( z ) É y = z ].

Аналогично, К., «ограниченный» каким-либо одноместным предикатом P ( x )( $ x P (x) , читается как «существует x , удовлетворяющий свойству Р и такой, что», а " x p ( x ) — «для всех х , удовлетворяющих свойству Р , верно, что»), легко выразить через К. общности и существования и операторы импликации и конъюнкции:

$ x p (x)A ( x ) º $ x [ P ( x )& A ( x )] и

" x p (x)A ( x ) º " x [ P ( x )É A ( x )].

Лит.: Клини С. К., Введение в метаматематику, пер. с англ., М., 1957, с. 72—80, 130—138; Чёрч А., Введение в математическую логику, пер. с англ., т. 1, М., 1960, с. 42—48.

Ю.А. Гастев.

Кванту'н,встречающееся в литературе на русском языке название юго-западной оконечности Ляодунского полуострова в Китае; см. Гуаньдун .

Кванту'нская а'рмия,группировка японских войск, предназначавшаяся для агрессии против Китая, СССР и МНР. Создана в 1931 на базе войск, расположенных на территории Квантунской области (юго-западной оконечности Ляодунского полуострова до залива Гуаньдун), откуда и получила своё название. 18 сентября 1931 К. а. вероломно напала на Китай и к началу 1932 оккупировала его северо-восточную провинцию — Маньчжурию, где было создано 9 марта 1932 марионеточное государство Маньчжоу-Го, ставшее фактически колонией японских империалистов и плацдармом для их последующей агрессии. Это событие положило начало серии вооружённых конфликтов с соседними странами, спровоцированных японской военщиной. Расширяя агрессию в Китае, японские империалисты одновременно стремились проверить прочность советских дальневосточных границ и овладеть выгодными плацдармами для последующего вторжения на территории СССР и МНР. Численность К. а. постепенно увеличивалась и к 1938 достигла 8 дивизий (около 200 тыс. человек), а в 1940—12 дивизий (около 300 тыс. чел.). Летом 1938 войска К. а. вторглись в пределы СССР у озера Хасан ; в 1939 была организована более крупная провокация против Советского Союза и МНР на р. Халхин-Гол , но в обоих конфликтах К. а. потерпела поражение. В 1941, когда советский народ вёл тяжёлую борьбу с фашистской Германией, К. а. в соответствии с японским планом « Кантокуэн » развернулась на маньчжурской границе и в Корее для нападения на СССР, выжидая удобного момента для начала боевых действий в зависимости от исхода борьбы на советско-германском фронте. В 1941—43 в Маньчжурии и Корее насчитывалось 15—16 японских дивизий (около 700 тыс. чел.).

К началу кампании Советских Вооруженных Сил на Дальнем Востоке (9 августа 1945) К. а. имела в своём составе: 1-й фронт (3-я и 5-я армии), 3-й фронт (30-я и 44-я армии), 17-й фронт (34-я и 59-я армии), отдельную (4-ю) армию, две (2-я и 5-я) воздушные армии и Сунгарийскую военную флотилию. Кроме того, ей были оперативно подчинены армия Маньчжоу-Го, войска Внутренней Монголии (князя Де Вана) и Суйюаньская армейская группа. В составе К. а. и подчинённых ей войск насчитывалось 37 пехотных и 7 кавалерийских дивизий, 22 пехотных, 2 танковых и 2 кавалерийских бригады (всего 1 млн. 320 тыс. человек), 1155 танков, 6260 орудий, 1900 самолётов и 25 кораблей. К. а. располагала также бактериологическим оружием, которое предназначалось для применения против Советских Вооруженных Сил. После разгрома К. а. в Маньчжурской операции 1945 Япония лишилась реальных сил и возможностей для продолжения войны и 2 сентября 1945 подписала акт о безоговорочной капитуляции.