БСЭ БСЭ - Большая Советская Энциклопедия (КР)
- Название:Большая Советская Энциклопедия (КР)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (КР) краткое содержание
Большая Советская Энциклопедия (КР) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Кратное
Кра'тноенатурального (целого положительного) числа а, натуральное число, делящееся на а без остатка. Так, 156 есть К. 13, тогда как 108 не является К. 13. Число n, которое делится на каждое из чисел а, b, ..., m, называется общим К. этих чисел. Из всех общих К. двух или нескольких чисел одно (не равное нулю) является наименьшим (наименьшее общее К.), а остальные будут К. этого наименьшего. К разысканию наименьшего общего К. приводит ряд задач арифметики. Чтобы найти наименьшее общее К. нескольких чисел, находят сначала наименьшее общее К. первых двух чисел, затем — наименьшее общее К. этого найденного и третьего числа и т. д. Зная наибольший общий делитель d двух чисел а и b, находят наименьшее общее К. т по формуле т = ab/d. Числа, кратные двум, называются чётными, остальные — нечётными.
Кратные единицы
Кра'тные едини'цы,единицы, которые в целое число раз больше системных или внесистемных единиц физических величин. В Международной системе единиц образование К. е. осуществляется по принципу десятичности в соотношениях К. е. с исходными единицами (см. также Дольные единицы ) . Наименование К. е. образуется из наименования исходной единицы с помощью приставок:
| Кратность | Приставка | Обозначение | |
| рус. | междунар. | ||
| 10 1 | дека | Да | Da |
| 10 2 | гекто | Г | H |
| 10 3 | кило | К | K |
| 10 6 | мега | М | М |
| 10 9 | гига | Г | G |
| 10 12 | тера | Т | Т |
Примеры: декалитр ( дал ) = 10 л, километр ( км ) = 10 3 м, мегагерц ( Мгц ) = 10 6гц и т. п.
Кратные звёзды
Кра'тные звёзды,система 3—7 близких друг к другу в пространстве звёзд, обращающихся вокруг общего центра масс под действием сил тяготения. Системы 8 и более звёзд большей частью являются ядрами звёздных скоплений. К. з. типа трапеции Ориона — системы с компонентами, расстояния между которыми примерно равны; такие К. з. могут быть неустойчивы. В некоторых случаях к К. з. может быть отнесена звезда, находящаяся значительно дальше или ближе системы и лишь проецирующаяся на неё на небе. Компоненты К. з. сами могут быть тесными двойными (спектральными, затменными и т. д.). В этом случае общее число звёзд в системе К. з. может оказаться больше 7. См. Двойные звёзды.
Кратные связи
Кра'тные свя'зи,тип химической связи, осуществляемой двумя или тремя парами электронов, общими для двух непосредственно соединённых атомов, как, например, в этилене H 2C = CH 2, формальдегиде H 2C = О, ацетилене HC º CH, синильной кислоте Н—С º N (подробнее см. Двойная связь. Тройная связь ) .
Кратный интеграл
Кра'тный интегра'л,интеграл от функции, заданной в какой-либо области на плоскости, в трёхмерном или n -мерном пространстве. Среди К. и. различают двойные интегралы, тройные интегралы и т. д. n -кратные интегралы.
Пусть функция f ( x, y ) задана в некоторой области D плоскости хОу. Разобьем область D на n частичных областей d i, площади которых равны s i, выберем в каждой области d i точку ( x i , h i ) (см. рис. ) и составим интегральную сумму
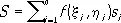 .
.
Если при неограниченном уменьшении максимального диаметра частичных областей d i суммы S имеют предел независимо от выбора точек ( x i , h i ), то этот предел называют двойным интегралом от функции f ( x, у ) по области D и обозначают
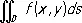 .
.
Аналогично определяется тройной интеграл и вообще n -кратный интеграл.
Для существования двойного интеграла достаточно, например, чтобы область D была замкнутой квадрируемой областью, а функция f ( x, y ) была непрерывна в D. К. и. обладают рядом свойств, аналогичных свойствам простых интегралов. Для вычисления К. и. обычно приводят его к повторному интегралу. В специальных случаях для сведения К. и. к интегралам меньшей размерности могут служить Грина формулы и Остроградского формула. К. и. имеют обширные применения: с их помощью выражаются объёмы тел, их массы, статические моменты, моменты инерции и т. п.
Лит. см. при статьях Интегральное исчисление, Интеграл.
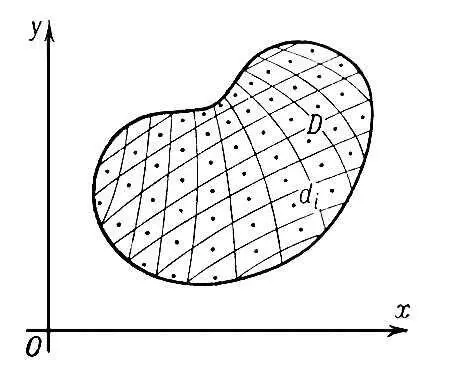
Рис. к ст. Кратный интеграл.
Кратный корень
Кра'тный ко'реньмногочлена
f ( x ) = a 0x n + a 1x n-1 +... + a n,
число с такое, что f ( x ) делится без остатка на вторую или более высокую степень двучлена ( х — с ) . При этом с называют корнем кратности, если f ( x ) делится на (х— с ) k , но не делится на ( х—c ) k+1. Корень многочлена f ( x ) кратности k является также корнем производных этого многочлена до ( k — 1)-го порядка включительно, т. е. многочленов f’ ( x ) , f'' ( x ) ,..., f ( k-1 )( x ) . К. к. многочлена f ( x ) называется К. к. уравнения f ( x ) = 0 . См. также Корень, Уравнение.
Кратных отношений закон
Кра'тных отноше'ний зако'н,закон Дальтона, один из основных законов химии: если два вещества (простых или сложных) образуют друг с другом более одного соединения, то массы одного вещества, приходящиеся на одну и ту же массу другого вещества, относятся как целые числа, обычно небольшие. К. о. з. открыт в 1803 Дж. Дальтоном и истолкован им с позиций атомизма. Примеры: 1) состав окислов азота (в процентах по массе) выражается следующими числами:
| Закись азота N 2O | Okись азота NO | Азотистый ангидрид Н 2Оз | Двуокись азота NO 2 | Азотный ангидрид N 2O 5 |
| N...63,7 | 46,7 | 36,8 | 30,4 | 25,9 |
| 0...36,3 | 53,3 | 63,2 | 69,6 | 74,1 |
| Частное 0/N...0,57 | 1,14 | 1,71 | 2,28 | 2,85 |
Разделив числа нижней строки на 0,57, видим, что они относятся как 1: 2: 3: 4: 5.
2) Хлористый кальций образует с водой 4 гидрата, состав которых выражается формулами: CaCl 2×H 2O, CaCl 2×2H 2O, CaCl 2×4H 2O, CaCl 2×6H 2O, т. е. во всех этих соединениях массы воды, приходящиеся на одну молекулу CaCl 2, относятся как 1: 2: 4: 6.
Кратон
Крато'н(от греч. krátos — сила, крепость), консолидированные участки земной коры, неспособные к преобразованию альпинотипной складчатостью (см. Альпинотипная тектоника ) . Немецким геологом Х. Штилле подразделялись на поднятые К. — массивы преимущественно сиалического (Si, Al) состава (древние докембрийские платформы или щиты советских геологов, характеризующиеся континентальным строением коры с развитым «гранитно-метаморфическим» слоем), и на погруженные К. — массивы с симатическим (Si, Fe, Mg) основанием (преимущественно области дна океанов, лишённые «гранитно-метаморфического» слоя земной коры). Термин «К.» предложен австрийским геологом Л. Кобером и широко применяется в зарубежной литературе.
Читать дальшеИнтервал:
Закладка:
