БСЭ БСЭ - Большая Советская Энциклопедия (ЛА)

Г. А. Чеботарев.

Лапла'са опера'тор, лапласиан, дельта-оператор, D-оператор, линейный дифференциальный оператор, который функции j(x 1, x 2,..., x n) от n переменных x 1, x 2,..., x nставит в соответствие функцию

Dj = .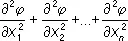

В частности, для функции j(x, y) двух переменных х, у Л. о. имеет вид

Dj = ,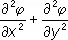

а для функций одной переменной j(x) Л. о. совпадает с оператором второй производной

Dj = .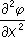

Л. о. встречается в тех задачах математической физики, где изучаются свойства изотропной однородной среды (распространение света, тепла, движение идеальной несжимаемой жидкости и т.п.).

Уравнение Dj = 0 обычно называется Лапласа уравнением; отсюда и произошло название Л. о.

Лапла'са преобразова'ние, преобразование, переводящее функцию f (t) действительного переменного t (0 < t < ¥), называемую «оригиналом», в функцию

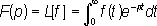(1)

комплексного переменного р =s +it. Под Л. п. понимают также не только само преобразование, но и его результат — функцию F ( p ). Интеграл в правой части формулы (1) называется интегралом Лапласа. Он был рассмотрен П. Лапласом в ряде работ, которые объединены в его книге «Аналитическая теория вероятностей», вышедшей в 1812. Значительно раньше (в 1737) такие интегралы применял к решению дифференциальных уравнений Л. Эйлер.

При некоторых условиях, указанных ниже, Л. п. определяет функцию f ( t ) однозначно, в простейших случаях — по формуле обращения:

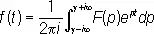(2)

Л. п. является линейным функциональным преобразованием. Из числа основных формул Л. п. можно отметить следующие:

,

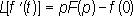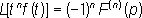, n = 1, 2, …,

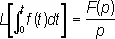, t >0.

Л. п. в сочетании с формулой (2) его обращения применяется к интегрированию дифференциальных уравнений. В частности, в силу свойства (1) и линейности, Л. п. решения обыкновенного линейного дифференциального уравнения с постоянными коэффициентами удовлетворяет алгебраическому уравнению 1-й степени и может быть, следовательно, легко найдено. Так, если, например, у’’ + у = f ( t ) , y (0) = y’ (0) = 0

и Y ( p ) = L [y], F ( p ) = L [f],

то L [y’’] = p 2Y ( p )

и p 2Y ( p ) + Y ( p ) = F ( p ) ,

откуда

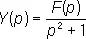
Многочисленные задачи электротехники, гидродинамики, механики, теплопроводности эффективно решаются методами, использующими Л. п.

Л. п. нашло особенно широкое применение в обосновании операционного исчисления, в котором обычно вместо Л. п. F (p) вводится «изображение» оригинала f ( t ) — функция pF ( p ) .

Современная общая теория Л. п. строится на основе интегрирования в смысле Лебега (см. Интеграл ) . Для применимости Л. п. к функции f ( t ) необходимо, чтобы f ( t ) была интегрируема в смысле Лебега на любом конечном интервале (0, t), t > 0 и интеграл (1) для неё сходился хотя бы в одной точке p 0 = s 0+ it 0. Если интеграл (1) сходится в точке р 0, то он сходится во всех точках р, для которых Re ( р—р 0 ) > 0. Т. о., если интеграл (1) сходится хотя бы в одной точке плоскости p 0, то либо он сходится во всей плоскости, либо существует такое число s с, что при Re p > s cинтеграл (1) сходится, а при Re р < s срасходится. Число s сназывается абсциссой сходимости интеграла Лапласа. F ( p ) — аналитическая функция в полуплоскости Re р > s с .

Лит.: Диткин В. А. и Кузнецов П. И., Справочник по операционному исчислению. Основы теории и таблицы формул, М. — Л., 1951; Диткин В. А. и Прудников А. П., Интегральные преобразования и операционное исчисление, М., 1961; Дёч Г., Руководство к практическому применению преобразования Лапласа, пер. с нем., М., 1965.

Лапла'са теоре'ма, простейшая из предельных теорем теории вероятностей, относящаяся к распределению отклонений частоты появления события при независимых испытаниях от его вероятности. В общем виде эта теорема доказана П. Лапласом в книге «Аналитическая теория вероятностей» (1812). Один частный случай Л. т. был известен А. Муавру (1730), в связи с чем Л. т. иногда называется теоремой Муавра — Лапласа. Формулировка Л. т. такова. Пусть при каждом из n независимых испытаний вероятность появления некоторого события Е равна р (0< р <1) и пусть m обозначает число испытаний, в которых событие Е фактически наступает; тогда вероятность неравенства

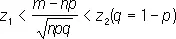
при достаточно большом числе испытаний n сколь угодно мало отличается от

.

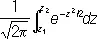Если обозначить через X kслучайную величину, принимающую значение, равное 1, при появлении события Е в k -ом испытании и значение, равное 0, при его непоявлении, то m представляется как сумма независимых случайных величин m = X 1+ ...+ X n. Это позволяет рассматривать Л. т. как частный случай более общих предельных теорем теории вероятностей, в частности Ляпунова теоремы.

Приближённые значения вероятностей, даваемые Л. т., на практике используются как точные при npq порядка нескольких десятков и большем.

Лит. см. при ст. Предельные теоремы теории вероятностей.

Ю. В. Прохоров.

Лапла'са уравне'ние, дифференциальное уравнение с частными производными

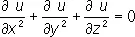
где х, у, z — независимые переменные, а u = u ( x, y, z ) — искомая функция. Это уравнение названо по имени П. Лапласа, рассмотревшего его в работах по теории тяготения (1782). К Л. у. приводит ряд задач физики и техники. Л. у. удовлетворяют температура при стационарных процессах, потенциал электростатического поля в точках пространства, свободных от зарядов, потенциал поля тяготения в области, не содержащей притягивающих масс, и т. п. Функции, удовлетворяющие Л. у., называются гармоническими функциями. О постановке задач для Л. у. см. в ст. Краевые задачи.