БСЭ БСЭ - Большая Советская Энциклопедия (ЛО)

Усреднение микроскопических величин производится по пространственным и временным интервалам, большим по сравнению с микроскопическими интервалами (порядка размеров атомов и времени обращения электронов вокруг ядра), но малым по сравнению с интервалами, на которых макроскопические характеристики электромагнитного поля заметно изменяются (например, по сравнению с длиной электромагнитной волны и её периодом). Подобные интервалы называются «физически бесконечно малыми».

Усреднение Л. — М. у. приводит к уравнениям Максвелла. При этом оказывается, что среднее значение напряжённости микроскопического электрического поля равно напряжённости поля в теории Максвелла: = Е , а среднее значение напряжённости микроскопического магнитного поля 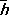— вектору магнитной индукции: 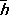= В .

В теории Лоренца все заряды разделяются на свободные и связанные (входящие в состав электрически нейтральных атомов и молекул). Можно показать, что плотность связанных зарядов определяется вектором поляризации Р (электрическим дипольным моментом единицы объёма среды):

r связ.= - div Р (2)

а плотность тока связанных зарядов, кроме вектора поляризации, зависит также от намагниченности I (магнитного момента единицы объёма среды):

j связ .= 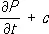rot I . (3)

Векторы Р и I характеризуют электромагнитное состояние среды. Вводя два вспомогательных вектора — вектор электрической индукции

D = E + 4p P (4)

и вектор напряжённости магнитного поля

H = B - 4p I (5)

получают макроскопические уравнения Максвелла для электромагнитного поля в веществе в обычной форме.

Помимо уравнений (1) для микроскопических полей, к основным уравнениям электронной теории следует добавить выражение для силы, действующей на заряженные частицы в электромагнитном поле. Объёмная плотность этой силы (силы Лоренца) равна:

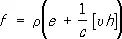(6)

Усреднённое значение лоренцовых сил, действующих на составляющие тело заряженные частицы, определяет макроскопическую силу, которая действует на тело в электромагнитном поле.

Электронная теория Лоренца позволила выяснить физический смысл основных постоянных, входящих в уравнения Максвелла и характеризующих электрические и магнитные свойства вещества. На её основе были предсказаны или объяснены некоторые важные электрические и оптические явления (нормальный Зеемана эффект, дисперсия света, свойства металлов и другие).

Законы классической электронной теории перестают выполняться на очень малых пространственно-временных интервалах. В этом случае справедливы законы квантовой теории электромагнитных процессов — квантовой электродинамики. Основой для квантового обобщения теории электромагнитных процессов являются Л. — М. у.

Лит.: Лорентц Г. А., Теория электронов и ее применение к явлениям света и теплового излучения, пер. с английского, 2 издание, М., 1953; Беккер Р., Электронная теория, перевод с немецкого, Л. — М., 1936; Ландау Л. Д. и Лифшиц Е. М., Теория поля, М., 1967 (Теоретическая физика, том 2).

Г. Я. Мякишев.

Ло'ренца преобразова'ния, в специальной теории относительности — преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой. Получены в 1904 Х. А. Лоренцом как преобразования, по отношению к которым уравнения классической микроскопической электродинамики ( Лоренца — Максвелла уравнения ) сохраняют свой вид. В 1905 А. Эйнштейн вывел их, исходя из двух постулатов, составивших основу специальной теории относительности: равноправия всех инерциальных систем отсчёта и независимости скорости распространения света в вакууме от движения источника света.

Рассмотрим частный случай двух инерциальных систем отсчёта å и å’ с осями х и x’, лежащими на одной прямой, и соответственно параллельными другими осями (у и y’, z и z’). Если система å’ движется относительно å с постоянной скоростью u в направлении оси х, то Л. п. при переходе от å к å’ имеют вид:

,

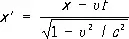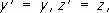
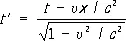
где с — скорость света в вакууме (штрихованные координаты относятся к системе å’, нештрихованные — к å).

Л. п. приводят к ряду важных следствий, в том числе к зависимости линейных размеров тел и промежутков времени от выбранной системы отсчёта, к закону сложения скоростей в теории относительности и др. При скоростях движения, малых по сравнению со скоростью света (u<< c ), Л. п. переходят в преобразования Галилея (см. Галилея принцип относительности ) , справедливые в классической механике Ньютона.

Подробнее см. Относительности теория ; см. также литературу при этой статье.

Г. А. Зисман.

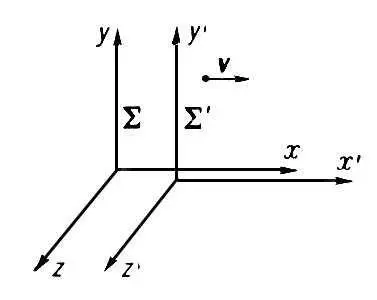
Рис. к ст. Лоренца преобразования.

Ло'ренца си'ла, сила, действующая на заряженную частицу, движущуюся в электромагнитном поле. Формула для Л. с. F была впервые получена Х. А. Лоренцом как результат обобщения опыта и имеет вид:

F = eE + [ u B].

Здесь е — заряд частицы, Е — напряжённость электрического поля, В — магнитная индукция , u — скорость заряженной частицы относительно системы координат, в которой вычисляются величины F , Е , В , а с — скорость света в вакууме. Формула справедлива при любых значениях скорости заряженной частицы. Она является важнейшим соотношением электродинамики, так как позволяет связать уравнения электромагнитного поля с уравнениями движения заряженных частиц.

Первый член в правой части формулы — сила, действующая на заряженную частицу в электрическом поле, второй — в магнитном. Магнитная часть Л. с. пропорциональна векторному произведению u и В , то есть она перпендикулярна скорости частицы (направлению её движения) и вектору магнитной индукции; следовательно, она не совершает механической работы и только искривляет траекторию движения частицы, не меняя её энергии. Величина этой части Л. с. равна u Bsin a, где a — угол между векторами u и В [множитель 1/ с связан с выбором единиц измерения: предполагается, что все величины измеряются в абсолютной (гауссовой) системе единиц ( СГС системе единиц ); в системе СИ этот множитель отсутствует]. Таким образом, магнитная часть Л. с. максимальна, если направление движения частицы составляет с направлением магнитного поля прямой угол, и равна нулю, если частица движется вдоль направления поля.