БСЭ БСЭ - Большая Советская Энциклопедия (ЛЕ)

В. Г. Клевцов.

Ле'ер(от голл. leier), судовой, трос, служащий для подъёма косых парусов, ограждения палубных отверстий или открытых палуб в местах, не защищенных комингсом или фальшбортом, подвески шлангов при передаче жидкого топлива на ходу и др. На современных судах постоянное или съёмное леерное ограждение состоит из металлических стоек высотой не менее 1 м, через отверстия которых пропускаются в 2—3 ряда Л.

Ле'жа, Олидовка, река в Вологодской области РСФСР, правый приток р. Сухона (бассейн Северной Двины). Длина 178 км, площадь бассейна 3550 км 2. Питание смешанное, с преобладанием снегового. Средний расход в 47 км от устья около 10,5 м 3/сек. Весеннее половодье с максимумом в конце апреля, летом и зимой межень. Замерзает в начале ноября, вскрывается в апреле — начале мая. Сплавная.

Лежа'ваАндрей Матвеевич [19.2(3.3).1870 — 8.10.1937], советский государственный и партийный деятель. Член Коммунистической партии с 1904. Родился в г. Сигнахи (Грузия) в семье крестьянина. Окончил Тбилисский учительский институт. В конце 80-х гг. примкнул к народническому движению. В 1893 арестован за участие в организации подпольной типографии в Смоленске, более 2 лет был в заключении в Петропавловской крепости, 5 лет в Якутской ссылке, где под влиянием Н. Е. Федосеева и др. стал марксистом. После ссылки вёл партийную работу в Тбилиси, Воронеже, Нижнем Новгороде (ныне Горький), Саратове, Москве. После Октябрьской революции 1917 на руководящей хозяйственной и советской работе. В 1919—20 председатель Центросоюза, в 1921—22 заместитель наркома внешней торговли, в 1922—24 нарком внутренней торговли. В 1924—30 заместитель председателя СНК РСФСР, одновременно председатель Госплана РСФСР, затем председатель треста Союзрыба. В 1930—1937 начальник Главного управления субтропических культур СССР. Делегат 10, 13—17-го съездов партии; на 15-м съезде избирался членом ЦКК. Член ВЦИК и ЦИК СССР ряда созывов.

Лежа'ндр(Legendre) Адриен Мари (18.9.1752, Париж, — 10.1.1833, там же), французский математик, член Парижской АН (1783). Л. обосновал и развил теорию геодезических измерений и первым открыл (1805—06) и применил в вычислениях наименьших квадратов метод. В области математического анализа им введены т. н. Лежандра многочлены, Лежандра преобразование и исследованы эйлеровы интегралы I и II рода. Л. доказал приводимость эллиптических интегралов (см. Эллиптические функции ) к каноническим формам, нашёл их разложения в ряды) составил таблицы их значений. Дал первое последовательное и полное изложение современной ему теории чисел. В вариационном исчислении установил признак существования экстремума. Написал известный учебник геометрии, в котором он безуспешно пытался доказать постулат о параллельных.

Соч.: Traité des fonctions elliptiques et dcs intégrales culériennes, t. 1—3, P., 1825—1828; Théorie des nombres, 4 éd., t. 1—2, P., 1855; в рус. пер. — Основания геометрии и тригонометрии, СПБ, 1837.

Лит.: Вилейтнер Г., История математики от Декарта до середины 19 столетия, пер. с нем., 2 изд., М., 1966.

А. М. Лежандр.

Лежа'ндра многочле'ны, сферические многочлены, специальная система многочленов последовательно возрастающих степеней. Впервые рассматривалась А. Лежандром и П. Лапласом (в 1782—85) независимо друг от друга. Для n = 0,1,2,... Л. м. Р ( х ) могут быть определены формулой:

,

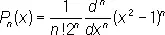в частности:

, , ,

,

,

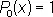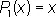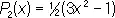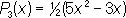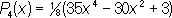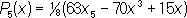
и т.д. Все нули многочлена P n ( x ) — действительные и лежат в основном промежутке [—1, +1], перемежаясь с нулями многочлена P n+i ( x ). Л. м. — ортогональные многочлены с весом 1 на отрезке [—1, +1,]; они образуют полную систему, чем обусловливается возможность разложения в ряд по Л. м. произвольной функции f ( x ), интегрируемой на отрезке [—1, +1]:

,

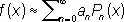где .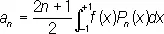

Характер сходимости рядов по Л. м. примерно тот же, что и рядов Фурье.

Явное выражение для Л. м.:

.

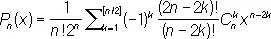Производящая функция:

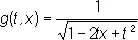
(Л. м. — коэффициенты при n -й степени в разложении этой функции по степеням t ). Рекуррентная формула:

nP n ( x ) + ( n - 1) P n-2 ( x ) - (2 n - 1) xP n-1 ( x ) = 0 .

Дифференциальное уравнение для Л. м.

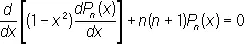
возникает при разделении переменных в уравнении Лапласа в сферических координатах. См. также Сферические функции.

Лит.: Янке Е., Эмде Ф., Лёш Ф., Специальные функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М., 1968; Лебедев Н. Н., Специальные функции и их приложения, 2 изд., М. — Л., 1963.

В. Н. Битюцков.

Лежа'ндра преобразова'ние,частный случай прикосновения преобразований; имеет вид:

Х = у' ( х ) , Y ( X ) = xy' ( x ) — y ( x ) , Y' ( X ) = x . Из этих формул вытекает, что и обратно x = Y' ( X ) , y ( x ) = XY' ( X ) -Y ( X ) , у' ( х ) =Х . Таким образом, Л. п. двойственно самому себе. Л. п. переводит дифференциальное уравнение первого порядка

F ( x, y, y' ) = 0 (1)

в уравнение

F ( Y', XY'-Y, x ) = 0, (2)

которое иногда интегрируется проще исходного. Зная решение уравнения (2), можно получить решение уравнения (1). Л. п. употребляется также при рассмотрении дифференциальных уравнений гидродинамики. Л. п. получило своё название по имени А. Лежандра, впервые изучившего его (1789).