БСЭ БСЭ - Большая Советская Энциклопедия (МА)

Лит.: Ленин В. И., Эсеровские меньшевики, Полное собрание сочинений, 5 изд., т. 13; Соколов М. И., Сущность максимализма, 2 изд., П., 1917; Задачи максимализма, в. 2, М., 1918; Жуков А. Ф., Разоблачение В. И. Лениным теории и тактики максимализма социалистов-революционеров, в книге: Идеи Ленина живут и побеждают, [Л.], 1970.

В. В. Гармиза, А. Ф. Жуков.

Максима'льного правдоподо'бия ме'тод,метод нахождения статистических оценок неизвестных параметров распределения; согласно М. п. м., в качестве оценок выбираются те значения параметров, при которых данные результаты наблюдений «наиболее вероятны». Предполагается, что результаты наблюдений X 1 , ..., X n являются взаимно независимыми случайными величинами с одним и тем же распределением вероятностей, зависящим от одного неизвестного параметра q Î Q, где Q — множество допустимых значений q. Для придания точного смысла принципу «наибольшей вероятности» поступают следующим образом. Вводят функцию

,

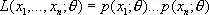где p ( t ; q) в случае непрерывного распределения интерпретируется как плотность вероятности случайной величины X , а в дискретном случае — как вероятность того, что случайная величина Х примет значение t . Функцию L ( X 1, . . ., Xn; q) от случайных величин X 1, . . ., X n называют функцией правдоподобия, а оценкой максимального правдоподобия параметра q называют такое значение 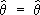( X 1, . . ., X n ) (само являющееся случайной величиной), при котором функция правдоподобия достигает наибольшего возможного значения. Так как точка максимума для log L та же, что и для L , то для нахождения оценок максимального правдоподобия следует решить так называемое уравнение правдоподобия

.

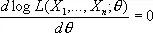М. п. м. не всегда приводит к приемлемым результатам, однако в достаточно широком круге практически важных случаев этот метод является в известном смысле наилучшим. Так, например, можно утверждать, что если для параметра q существует несмещенная эффективная оценка q* по выборке объёма n , то уравнение правдоподобия имеет единств, решение 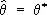. Что касается асимптотического поведения оценок максимального правдоподобия при больших n , то известно, что при некоторых общих условиях М. п. м. приводит к состоятельной оценке, которая асимптотически нормальна и асимптотически эффективна. Данные выше определения непосредственно обобщаются и на случай нескольких неизвестных параметров и на случай выборок из многомерных распределений. М. п. м. в его современном виде был предложен английским статистиком Р. Фишером (1912), однако в частных формах метод использовался К. Гауссом, а ещё раньше, в 18 веке, к его идее были близки И. Ламберт и Д. Бернулли. Следует добавить, что название «М. п. м.» является калькой с английского «maximum likelihood method».

Лит.: Крамер Г., Математические методы статистики, перевод с английского, М., 1948; Рао С. Р., Линейные статистические методы и их применения, перевод с английского, М., 1968; Худсон Д., Статистика для физиков, перевод с английского, М., 1970.

А. В. Прохоров.

Максимиа'нМарк Аврелий Валерий (Marcus Aurelius Valerius Maximianus) (240—310), римский император в 286—305 и 307—310. Сын крестьянина из Паннонии, М. дослужился до высоких чинов на военной службе. В 285 Диоклетиан провозгласил его цезарем, а в 286 — августом, своим соправителем. М. отличился особой жестокостью при подавлении восстаний багаудов в Галлии (285) и германских племён (286). В 290—291 отразил наступление мавретанских племён в Африке. Поддерживал реформы Диоклетиана. В 305 вместе с Диоклетианом отрекся от престола, но в 307 вновь объявил себя августом. Убит (по официальной версии, покончил жизнь самоубийством) в ходе борьбы за власть.

Максимилиа'н(Maximilian). В «Священной Римской империи»:

М. I(22.3.1459, Винер-Нёйштадт, — 12.1.1519, Вельс), император с 1493, австрийский эрцгерцог. Из династии Габсбургов. Сын и преемник императора Фридриха III. Путём брака с Марией Бургундской (1477) приобрёл Нидерланды и Франш-Конте. Использовал брачные союзы для обеспечения за своими наследниками испанского, венгерского и чешского престолов. М. I положил начало реальному объединению австрийских владений Габсбургов, централизации их управления. Напротив, предпринятая при М. I имперская реформа (решения германских рейхстагов 1495 и 1500 о создании общеимперских судебных и административных учреждений, провозглашение «земского мира» и др.) оказалась малоэффективной из-за сохранявшегося всевластия князей. Потерпев поражение в так называемой Швабской войне со швейцарцами (1499), М. I вынужден был признать окончательное отделение Швейцарии от империи; неудачным было и вмешательство М. I в итальянские войны 1494 — 1559. При М. I были завязаны дипломатические отношения с Русским государством.

М. II(1.8.1527, Вена, — 12.10.1576, Регенсбург), император с 1564, австрийский эрцгерцог. Сын императора Фердинанда I. По разделу земель между членами дома Габсбургов (1564) получил Верхнюю и Нижнюю Австрию и корону Чехии и Венгрии. Всецело завися в финансовых вопросах от австрийских, чешских и венгерских феодалов, вынужден был сделать им значительные уступки; при нём в габсбургских землях широко распространился протестантизм.

Максимилиан I(Maximilian) Габсбург (6.7.1832, Вена, — 19.6.1867, Керетаро, Мексика), император Мексики в 1864—1867, австрийский эрцгерцог. Брат австрийского императора Франца Иосифа I. В 1857—1859 генерал-губернатор австрийских владений в Италии. В период англо-франко-испанской интервенции в Мексику, имевшей целью свержение прогрессивного правительства Б. Хуареса (см. Мексиканская экспедиция 1861—1867 ) , М. I, являясь ставленником французского императора Наполеона III, был возведён на мексиканский престол (апрель 1864). Власть М. I распространялась только на районы, оккупированные французскими войсками. В марте 1867 французские войска покинули Мексику, в мае армия консерваторов, поддерживавшая М. I, была разгромлена мексиканской народной армией, а М. I взят в плен; судом военного трибунала приговорён к смертной казни и расстрелян.

Максимилиан I. Портрет работы А. Дюрера.